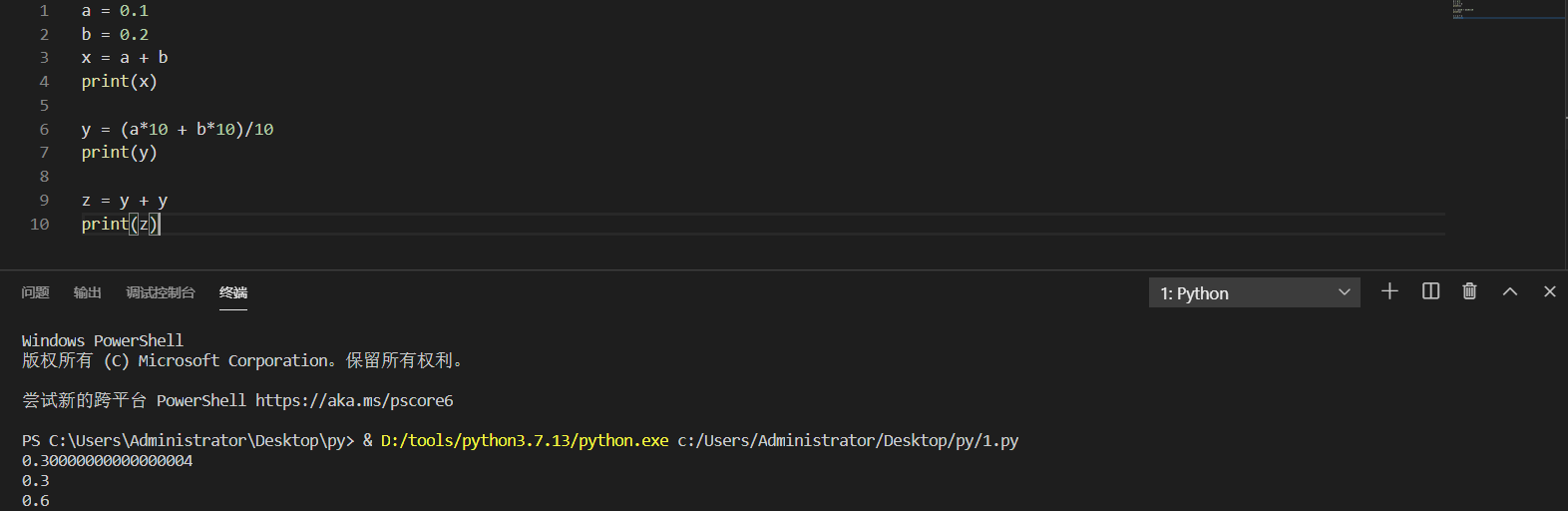
最近在学习JS过程中发现了一个非常有意思事,就是运算0.1+0.2的结果不是0.3,而是0.30000000000000004,但先将小数做乘法然后相加,再除回来就得到想要的0.3

我用python试了一下,发现python也是一样的,结果也是0.30000000000000004。
然后我开始信息搜集,最后找到了答案。想知道这其中的原因,要先理解这些点:二进制、指数形式、IEEE 754标准。
1、二进制
在计算机中所有的数据都是二进制形式存储的,包括整数、浮点数以及其他所有类型的数据。我们将十进制的0.1以及0.2转换成二进制
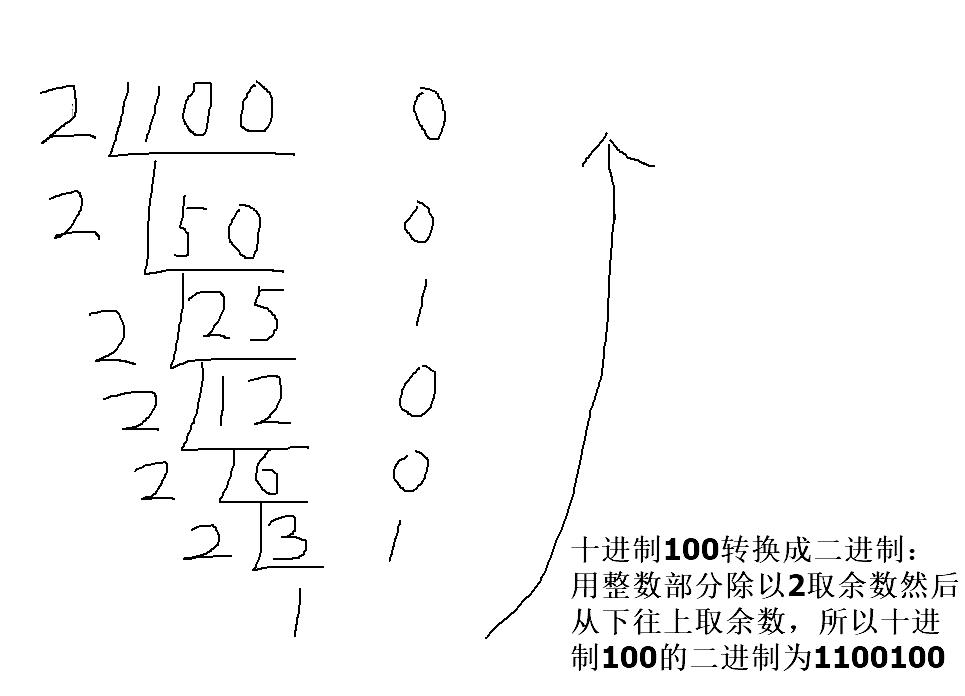
转换的方法也比较简单,整数转换成二进制:就是用整数除以2然后从下往上取余数,下图用100举例
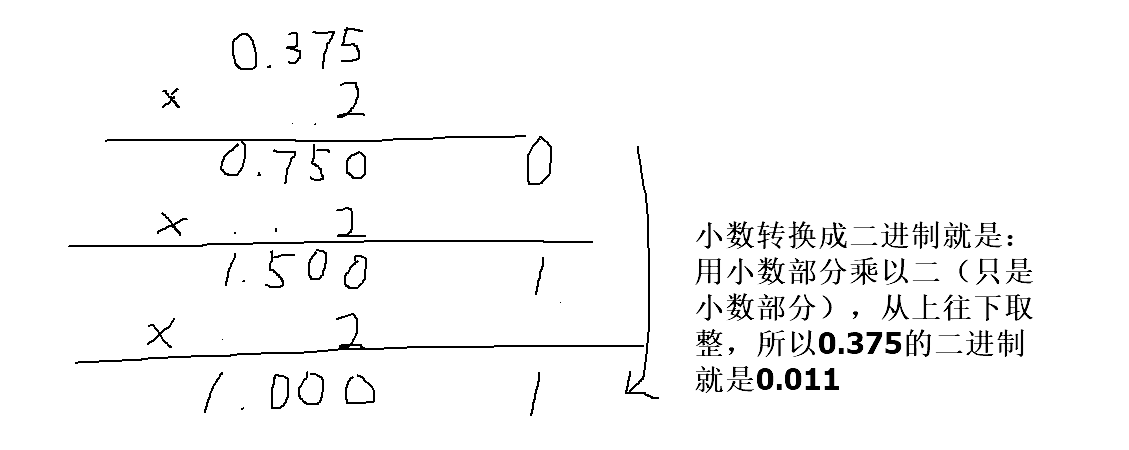
然后小数转换成二进制就是,小数部分无限乘以2,然后顺序取整。下图用0.375举例
2、指数形式
用指数方式表示可以在有限的空间里存储更大的数值。
所有的十进制数都可以用指数形式表示,成为D=M*10E,比如100可以表示为1*102。
二进制数也可以用指数形式表示,B=M*2E的形式,这里的E为指数,M为B的位数。比如0.011可以表示为1.1*10-10,这里的“-10”表示的是-2。
3、浮点数IEEE754标准
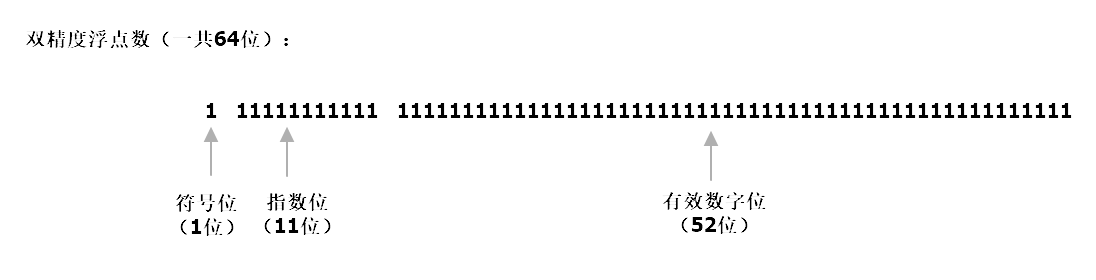
IEEE 754规定,对于规定了四种表示浮点数值的方式:单精确度(32位)、双精确度(64位)、延伸单精确度(43比特以上,很少使用)与延伸双精确度(79比特以上,通常以80位实现) //后两个今天不作研究
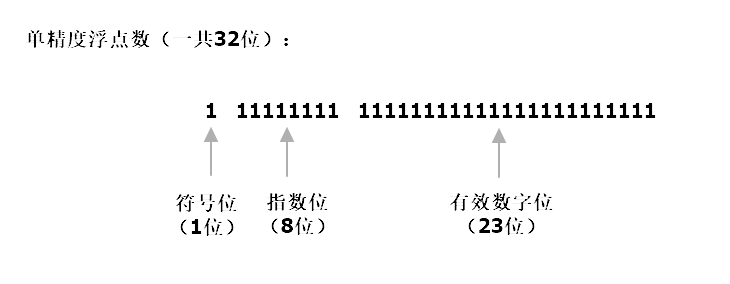
所有的二进制数V都可以用{S,E,M}表示,也就是V=(-1)S×1.M×2E
符号位 S(Sign)能够决定二进制数是正数,(-1)S所以当S为1时结果就是负数,S为0时结果就是正数。(而数值0的符号位会比较特殊)
有效数字位M(Significand)是二进制小数,它的取值范围是1≤1.M<2,大于等于1小于2也就是1.XXXXXXXXX......(单精度是23位,双精度是52位),由于有效数字位的取值整数位永远是1,所以可以被舍去,保留后面的XXXXXXX.....部分,这样就节省了一位有效数字。
指数位 E(Exponent)是 2 的幂(单精度是8位,双精度是52位)是一个无符号整数,就是说它一定是正整数。比如现在E的长度为8位,E的取值范围就是0——255(因为最小就是八个0,最大就是八个1);长度为11位,E的取值范围就是0——2047。但是由于指数位是可以存在负数的,所以为了表达出指数的负数形式设计出了偏移量(单精度137,双精度1023),用E真实的数值加上偏移量计算出指数位(也可以理解为1023表示的是0,小于1023就是负数,大于1023就是正数)。
下面以0.375举例

对于指数的值全部为0或者1的情况IEEE 754有特殊规定:
当指数全部为1,有效数字全部为0时,表示的就是正0和负0:
+0:0 00000000000 0000000000......一共64个0
-0:1 00000000000 0000000000......一共63个0
但它其实并不是精确的0,只是最接近0的数值,因为它的值是
V=(-1)^S×1.M×2^E :(-1)0*1.00000000000......*2-1023,有效数字为这里永远默认有个1
当指数全部为1时,如果有效数字M全为0,表示±无穷大;如果有效数字M不全为0,表示这个数不是一个数(NaN)。
V=(-1)^S×1.M×2^E :(-1)0*1.00000000000......*21023 //正负取决于S
JavaScript中所有数字包括整数和小数都只有一种类型,是遵循 IEEE 754 标准,使用64位固定长度来表示,也就是标准的 double 双精度浮点数。
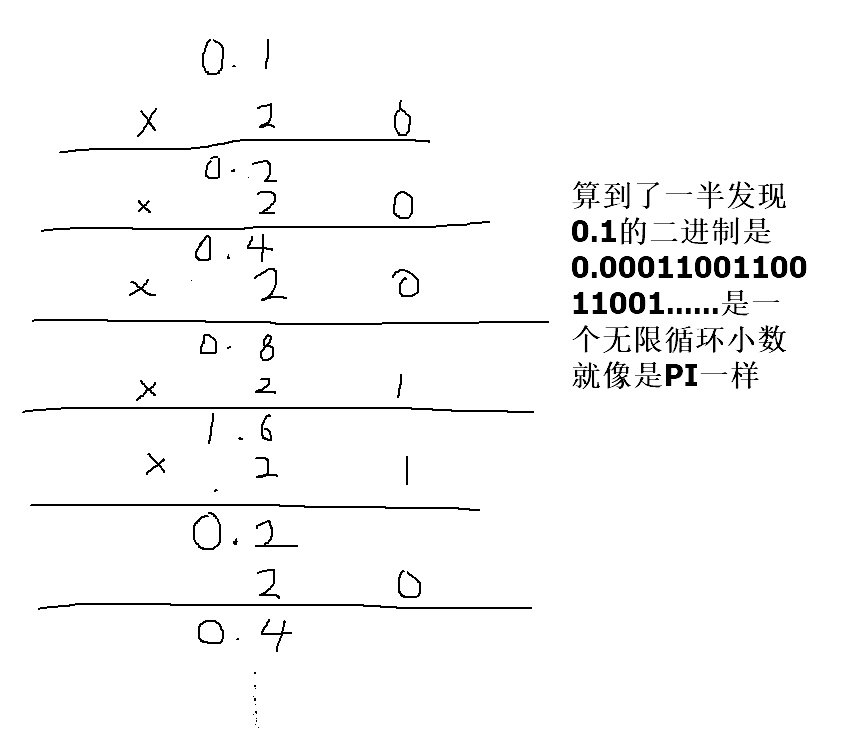
一、首先将十进制的0.1转换成二进制:0.0011001100110011......
然后将十进制的0.2转换成二进制:0.0011001100110011........
二、将二进制的0.1和0.2转换成指数形式
十进制:0.1
二进制形式:0.000110011001100110011......
指数形式:1.10011001100110011......*2-100 //指数是-4
十进制:0.2
二进制形式:0.001100110011001100110011......
指数形式:1.100110011001100110011......*2-11 //指数是-3
三、将指数形式转换为IEEE754标准
这里由于IEEE754标准规定了尾数只能保留52位,所以无限循环小数需要做四舍五入,只保留52位小数(就是第53位以后全部舍弃,第53位“0舍1入”,而当第52位为1时,还得再进一位)

将十进制0.2转换成IEEE 754标准:

四、使用IEEE 754形式的 0.1+0.2 (简单写了)

简单写的话应该就是10.0100100100100100100100100100100......100111,但是此时得到的数指数依然是指数形式,要将它转换成为二进制形式,就是将小数点向前移三位变成0.01001001001001001001001.....00111
然后将这个数转换为十进制数就是0*2-1+1*2-2+0*2-3+0*2-4.......+1*2-52之后就可以得到0.30000000000000004了
总结一下就是:
计算机存储数据时由于空间有限,所以只能存储固定长度的数据,而像一些无限循环的数据只能被四舍五入,所以一些数据可能会和它本身有一些误差,所以做相加运算也会有误差。
那么最后再看一下(0.1*10+0.2*10)/10为什么等于3,由于0.1和0.2先做乘法运算所以就变成了整数形式,所以有效数字为全部变成了0,避免了计算时的误差,所以就的到了想要的0.3。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号