迪利克雷分布

 概率单纯形网址：https://zhuanlan.zhihu.com/p/479892005

狄利克雷分布（Dirichlet distribution）或多元Beta分布（multivariate Beta distribution）是一类在实数域以正单纯形（standard simplex）为支撑集（support）的高维连续概率分布，是Beta分布在高维情形的推广 [1]  。支撑集是最小的x集合且f(x)!=0，支撑集为单纯形，说明迪利克雷分布为单纯形。

概率单纯形（probability simplex）是一个数学空间，其中的每个点代表有限个互斥事件之间的概率分布。每个事件通常被称为一个类别，我们通常使用变量K来表示类别的数量。

概率单纯形上的一个点可以用K个之和为1的非负数表示。以下是一些例子：

在 K=2 的单纯形上的点: (0.6, 0.4)。

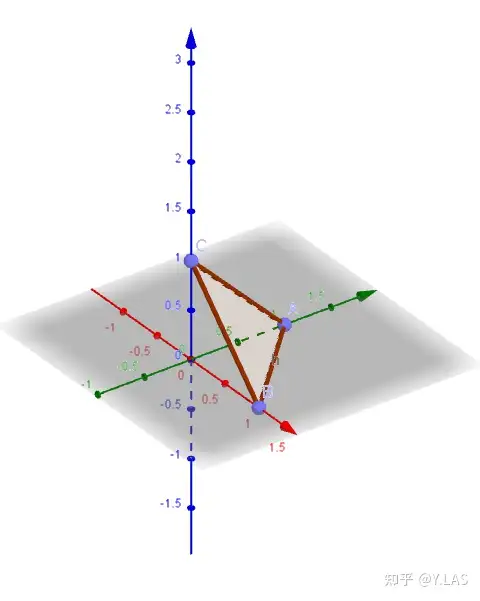
在 K=3 的单纯形上的点: (0.1, 0.1, 0.8)。

在 K=6 的单纯形上的点: (0.05, 0.2, 0.15, 0.1, 0.3, 0.2)。

当K=2时，这个空间是直线，当K=3时，它是三角形，当K=4时，它是四面体。和为1的条件将维数减少1，因此在每种情况下，单纯形都是（K-1）维对象。

概率单纯形在贝叶斯推理中非常常见。例如，如果我们要在假设A、B和C之间做出选择，记我们的假设空间为{A、B、C}。我们所相信的关于假设A、B或C为真的可能性属于概率单纯形，其中K=3。

概率单纯形的每个“角”或“顶点”表示所有概率都放在某一个类别上的情况。例如，在上面假设空间为{A，B，C}的情况下，点{A=0，B=1，C=0}代表所有概率都放在B上的情况。

如果一个假设被判定为不可能（即概率为零），那么其他K-1个假设的概率总和为1，因此K维单纯形的“边界”实际上是一个K-1维单纯形。

在博弈论中，智能体关于K个不同的潜在行为的“混合策略”是一个K维单纯形。