P5303 题解
题意简述
$T$ 次询问。每次给出一个正整数 $n(1\le n\le 2\times 10^9)$，表示有 $n-1$ 块 $2\times 1$ 的砖和 2 块 $1\times 1$ 的砖，求在两块 $1\times 1$ 的砖没有边相邻的前提下，用所有砖铺满 $2\times n$ 的路面的方案种数。
题目分析
注意到 $1\le n\le 2\times 10^9$，考虑用矩阵快速幂优化 DP。
我们很自然地想到使用 $F_k$ 表示 $n=k$ 时的种数。考虑状态转移方程。
显然，$n=k+1$ 比 $n=k$ 只在边界多了一列。将铺满这一列的形式分类讨论：
- 使用一块竖着的 $2\times 1$ 的砖。
显然铺满的种类就是左边 $2\times (n-1)$ 区域铺满的种数，即 $F_{n-1}$
- 使用两块横着的 $2\times 1$ 的砖。
铺满的种类就是左边 $2\times (n-2)$ 区域铺满的种数，即 $F_{n-2}$
- 使用 $1\times 1$ 的砖。
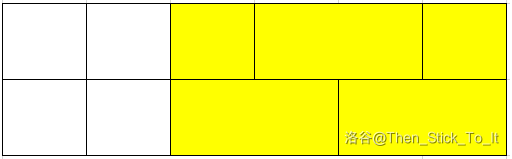
很明显这块砖可以摆在上下两种位置。以摆在上面为例，那么由于两块 $1\times 1$ 的砖不能相邻，下面只能使用一块横着的 $2\times 1$ 的砖；同样这块 $1\times 1$ 的砖的左侧只能使用一块横着的 $2\times 1$ 的砖。而再往左也是同样，横着的 $2\times 1$ 的砖上下位置交替，摆到某块时使用另一块 $1\times 1$ 的砖。
注意到使用另一块 $1\times 1$ 的砖之后，这块砖的右侧部分是固定的（只有 1 种摆法），因此铺的种数是只使用 $1\times 2$ 的砖铺满左侧区域的种数。
设 $G_i$ 代表用 $i$ 块 $1\times 2$ 的砖铺满 $2\times i$ 的路面的种数。
经过上文类似的讨论可以得到$G$ 的递推公式 $G_0=1,G_1=1,G_i=G_{i-1}+G_{i-2}$。
回到原题，由于 $2\times 1$ 的砖摆 $k$ 块时左侧区域为 $2\times (n-k-1)$，种数也就是 $G_{n-k-1}$。再考虑到第 1 块砖有两种摆放方式，因此第 3 种情况的种数就是 $2\displaystyle\sum_{k=2}^{n-1}G_{n-k-1}=2\sum_{k=0}^{n-3}G_k=2S_{n-3}$，其中 $S_{n-3}$ 代表 $G_{i}$ 从第 0 项到第 $n-3$ 项之和。
综上，有递推公式 $F_{n}=F_{n-1}+F_{n-2}+2S_{n-3}$，设计答案矩阵为 $\begin{bmatrix} F_n & F_{n-1} & S_{n-2} & G_{n-2} & G_{n-3} \end{bmatrix}$，其初始值 为$\begin{bmatrix} F_3=2 & F_2=0 & S_1=2 & G_1=1 & G_0=1 \end{bmatrix}$ 。为了将答案矩阵拓展到 $\begin{bmatrix} F_{n+1} & F_n & S_{n-1} & G_{n-1} & G_{n-2} \end{bmatrix}$ 转移矩阵为：
$$ \begin{bmatrix} 1 & 1 & 0 & 0 & 0\\ 1 & 0 & 0& 0 & 0\\ 2 & 0 & 1& 0 & 0\\ 0 & 0 & 1 & 1 & 1\\ 0 & 0 & 1 & 1 &0 \end{bmatrix} $$
我们对转移矩阵一列一列地来解释。
对于第一列，有 $F_{n+1}=1F_n+1F_{n-1}+2S_{n-2}+0G_{n-2}+0G_{n-3}$
对于第二列，有 $F_n=1F_n+0F_{n-1}+0S_{n-2}+0G_{n-2}+0G_{n-3}$
对于第三列，有 $S_{n-1}=S_{n-2}+G_{n-1}=0F_n+0F_{n-1}+1S_{n-2}+1G_{n-2}+1G_{n-3}$
对于第四列，有 $G_{n-1}=0F_n+0F_{n-1}+0S_{n-2}+1G_{n-2}+1G_{n-3}$
对于第五列，有 $G_{n-2}=0F_n+0F_{n-1}+0S_{n-2}+1G_{n-2}+0G_{n-3}$
现在我们只需要计算出转移矩阵的 $n-3$ 次幂，再乘到答案矩阵上就好了。
需要注意的是要特判 $n\le2$，否则会挂掉。
分析一下时间复杂度。一次矩阵乘法是 $O(5^3)=O(125)$，因此矩阵快速幂的时间复杂度为 $O(125\log n)$，总复杂度为 $O(125T\log n)$，在 $T\le 500,1\le n\le 2\times10^{9}$，时限 $1.00s$ 的情况下是可以通过的。
代码实现
#include<bits/stdc++.h>
using namespace std;
const int mod=1000000007;
int t,n;
struct matrix
{
int n,m;
int a[6][6];
void init(int k)
{
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(i!=j)
a[i][j]=0;
else
a[i][j]=k;
}//初始化矩阵，k=0是零矩阵，k=1为单位矩阵
friend matrix operator *(matrix a,matrix b)
{
matrix c;
c.n=a.n,c.m=b.m;
c.init(0);
for(int i=1;i<=c.n;i++)
for(int j=1;j<=c.m;j++)
for(int k=1;k<=b.n;k++)
(c.a[i][j]+=1ll*a.a[i][k]*b.a[k][j]%mod)%=mod;
return c;
}//矩阵乘法
friend matrix operator ^(matrix a,int b)
{
matrix c;
c.n=c.m=a.n;
c.init(1);
for(;b;b>>=1)
{
if(b&1)
c=c*a;
a=a*a;
}
return c;
}//矩阵快速幂
}fs,tr;
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
if(n<=2)//特判
{
printf("0\n");
continue;
}
fs.n=1,fs.m=tr.n=tr.m=5;
fs.init(0);
fs.a[1][5]=fs.a[1][4]=1;
fs.a[1][1]=fs.a[1][3]=2;//答案矩阵初始化
tr.init(0);
tr.a[1][1]=tr.a[2][1]=tr.a[1][2]=tr.a[3][3]=tr.a[4][3]=tr.a[4][4]=tr.a[4][5]=tr.a[5][3]=tr.a[5][4]=1;
tr.a[3][1]=2;//转移矩阵初始化
tr=tr^(n-3);
fs=fs*tr;
printf("%d\n",fs.a[1][1]);
}
return 0;
}