UVA1453题解
作为一道旋转卡壳好题,题解只有随机化乱搞做法,这我不能忍
题意简述
给定平面上 $n$ 个边平行于坐标轴的正方形,求出这些正方形的顶点之间距离最大的两个点的距离的平方。
题目分析
显然, 这是一道旋转卡壳的题目,在解题之前,先来了解一下旋转卡壳是什么。

注意,本题解将凸包作为前提知识之一,并默认使用 Andrew 算法。不了解凸包的话请出门左转百度。
回归主题,接下来是具体过程。
- 用两条平行线把凸包“卡”住,如下图:
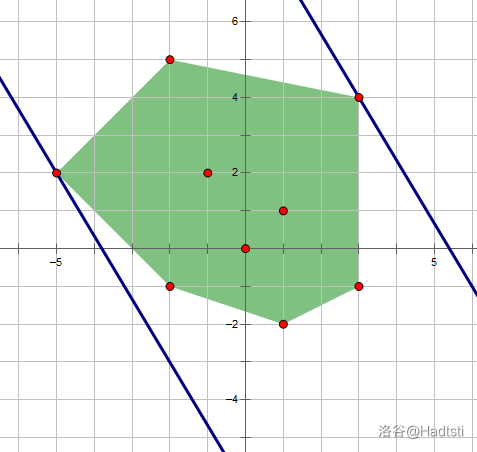
2.旋转平行线,并让其不断“卡壳”,直到旋转 180°(与平行线初始位置重合)时。
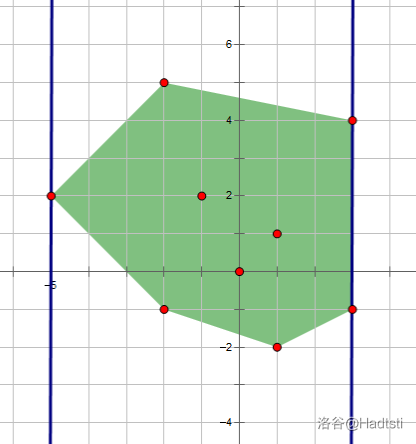
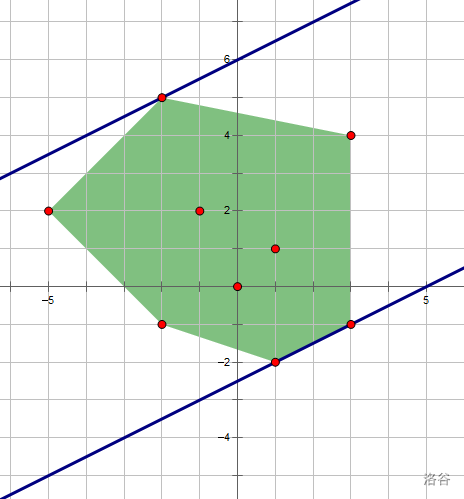
3.我们将平行线“卡”住的两个(或 3、4 个)点称为对踵点。那么,在旋转卡壳过程中每对对踵点的距离取最大值就是答案。
听起来很简单,是不是?但是实际上要复杂的多。这是因为旋转靠的是角度的变化,但是角度是连续的,无法枚举。所以我们要使用另外的方式计算旋转卡壳的答案。
首先,很明显的是,在旋转卡壳过程中,对踵点的变化都是在凸包的一条边与平行线中的一条重合时发生的。换句话说,旋转卡壳可以缩略为不断固定凸包上的边,求与其距离最大的点的过程。于是我们的思路一下清晰了很多——显然,从凸包的一条边开始,不断选它相邻(这里假设是左侧)的边,与当前边距离最远的点一定也在上一个距离最远的点右侧(不一定相邻),从刚才的图中其实也可以看出这一点。
所以,我们可以依照这个特点设计一个双指针算法:两个变量 $i$ 和 $j$,分别表示当前边(凸包中编号为 $i$ 和 $i+1$ 的点之间连接的边)和与当前边距离最大的点(注意不是编号)。每次当 $i$ 变为 $i+1$ 时,不断将 $j$ 改为 $j+1$,并将其与原先的 $j$ 到 $i$ 与 $i+1$ 之间的边的距离作比较,直到距离取到最大值时定下 $j$。至于两点到线段之间的距离比较,我们可以用叉积,也就是将 $Cross((i+1)-i,j-i)$ 与 $Cross((i+1)-i,(j+1)-i)$ 作比较。那么我们就可以在此过程中计算出相应对踵点之间的距离并取其中的最大值,也就是相应 $i$ 对应的 $max(Distance(i,j),Distance(i+1,j))$。
另外有两个小细节:
第一个是当 $i$ 取到 $n$ 时,$i+1$ 要取模么?答案是不用。注意到凸包是“转了一圈的”,所以所谓编号为 $n+1$ 的点与编号为 $1$ 的点是重合的,而这在求凸包过程中已经体现了出来(至少是在我的 Andrew 写法中),这是一个比较有趣的小 trick。
第二个是比较 $Cross((i+1)-i,j-i)$ 与 $Cross((i+1)-i,(j+1)-i$ 的大小。我们都知道,有 $Cross(A,B) - Cross(A,C) = Cross(A,B-C)$,那么有:$$Cross((i+1)-i,(j+1)-i)-Cross((i+1)-i,j-i)=Cross((i+1)-i,(j+1)-j)$$ 即判断 $Cross((i+1)-i,j-i)$ 与 $Cross((i+1)-i,(j+1)-i$ 的大小,比较 $Cross((i+1)-i,(j+1)-j)$与 0 的大小即可。
那么旋转卡壳的基本过程就是这样,至于本题,将每个正方形的顶点都提出来算一个凸包直径即可,思路比较直接。
代码较复杂,结合注释理解。
代码实现
#include<bits/stdc++.h>
using namespace std;
int t,x,y,w,n;
void rd(int &x)
{
x=0;
int f=1;
char c=getchar();
for(;c>'9'||c<'0';c=getchar())
if(c=='-')
f=-1;
for(;c>='0'&&c<='9';c=getchar())
x=(x<<3)+(x<<1)+c-'0';
x*=f;
}
struct Vector
{
int x,y;
Vector(int x=0,int y=0):x(x),y(y){}
friend Vector operator-(Vector a,Vector b)
{
return Vector(a.x-b.x,a.y-b.y);
}
friend bool operator<(Vector p1,Vector p2)
{
return p1.x<p2.x||(p1.x==p2.x&&p1.y<p2.y);
}
friend bool operator==(Vector p1,Vector p2)
{
return p1.x==p2.x&&p1.y==p2.y;
}
};
typedef Vector Point;
vector<Point>pt;
int Cross(Vector A,Vector B)
{
return A.x*B.y-A.y*B.x;
}//叉积
int Diss(Point A,Point B)
{
return(A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y);
}//两点距离的平方
int Diameter(vector<Point>& p)
{
//先求凸包
sort(p.begin(),p.end());
p.erase(unique(p.begin(),p.end()),p.end());
int n=p.size();
int m=0;
vector<Point>ch(n+1);
for(int i=0;i<n;i++)
{
while(m>1&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0)
m--;
ch[m++]=p[i];
}
int k=m;
for(int i=n-2;i>=0;i--)
{
while(m>k&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0)
m--;
ch[m++]=p[i];
}
if(n>1) m--;
ch.resize(m);
n=ch.size();
if(n==1)
return 0;//特判凸包退化为点
if(n==2)
return Diss(ch[0],ch[1]);//特判凸包退化为线段
ch.push_back(ch[0]);//由于换了 Andrew 模板(教练让的),凸包没有加上最后一条边,仍需要模。
int ans=0;
for(int u=0,v=1;u<n;u++) //u 是分析中的 i,v 是分析中的 j。
while(1)
{
int diff=Cross(ch[u+1]-ch[u],ch[v+1]-ch[v]);
if(diff<=0) //判断 Cross((i+1)-i,j-i) 与 Cross((i+1)-i,(j+1)-i 的大小
{
ans=max(ans,Diss(ch[u],ch[v]));
if(diff==0)//如果 i 与 i+1 之间的边和 j 与 j+1 之间的边平行,卡壳时会一起被“卡”住,j 与 j+1 同时距离 i 与 i+1 之间的边最远,需要把 j+1 作为对踵点再更新一下答案。
ans=max(ans,Diss(ch[u],ch[v+1]));
break;
}
v=(v+1)%n;//如果 j 距离 i 与 i+1 之间的边不是最远的,把 j 变为 j+1 继续计算。
}
return ans;
}
int main()
{
rd(t);
while(t--)
{
pt.clear();
rd(n);
for(int i=1;i<=n;i++)
{
rd(x),rd(y),rd(w);
pt.push_back(Point(x,y)),pt.push_back(Point(x+w,y));
pt.push_back(Point(x,y+w)),pt.push_back(Point(x+w,y+w));//加入四个顶点
}
printf("%d\n",Diameter(pt));
}
return 0;
}这是本蒟蒻的第六篇题解,求管理大大过了吧

