Math Common Sense 数学小常识

The sum of arithmetic sequence

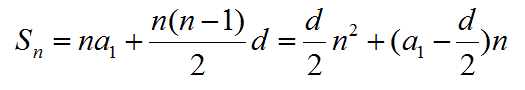
The sum of geometric sequence

 

 

A special formula : n·n! = (n+1)! - n!

 

Divisible Test

4: The last 2 digits are divisible by 4

6: Divisible by both 2 and 3

7: Truncate the final digit. Use the rest minus the final digit truncated twice. Check the answer if can be divisible by 7. [ truncation, double, distraction, check ]

8: The last 3 digits are divisible by 8

9: Sum of digits is divisible by 9

11: Add and subtract digits alternating from left to right. Check the answer if can be divisible by 11

　　913 ( 9 - 1 + 3 = 11 yes )

　　1364 ( 1 - 3 + 6 - 4 = 0 yes )

　　987 ( 9 - 8 + 7 = 8 no )

　　3729 ( 3 - 7 + 2 - 9 = -11 )

 

The number of divisors 

72 = 2³ x 3²

( 3 + 1 ) x ( 2 + 1 ) = 12

Each exponent plus one and multiply together

 

The factor of polynomial

a₁xⁿ + a₂x^n-1 + ······ + a_nx + k = 0

if it can divide by ( x - s ) , then s is a factor of k/a₁

a3 - 8a + 8 = 0

8/1 = 8 → ±1, ±2, ±4, ±8

 

Vieta's theorem

ax3 + bx2 + cx + d = 0

x1 + x2 + x3 = -b/a

x1x2 + x1x3 + x2x3 = c/a

x1x2x3 = -d/a

  

Entire radical : the coefficient is one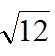 

 

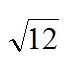
Mixed radical : 

 

f(x) ÷ (x-a) = quotient  ······ f(a)

if f(a) = 0, f(x) is divisible by (x-a)

Ex.1. What's the remainder of (5x³ + 4x² - 12x + 1) ÷ (x - 3)

5·3³+4·3²-12·3+1=136

Ex.2. What's the remainder of (x4+x) ÷ (x2-3x+2)

let ax+b be the remainder ( the degree of remainder is less 1 than divisor's )

Solve the divisor, x=1,2

(1⁴+1) = a·1+b

(2⁴+2) = a·2 +b

→ a=16, b=-14

therefore the remainder is 16x-14

 

Theorem about Secant, Tangent and Arc