POJ3233_Matrix Power Series_矩阵幂_C++

　　题目：http://poj.org/problem?id=3233

 

　　这是今天考试的题目，结果没想出来写了个暴力30分，看完题解之后觉得自己是SB

　　

 

　　首先暴力就是一个个乘然后相加，时间是O(kn3)，极限数据要跑一个月才跑得出来

　　我们思考，求幂的话有快速幂（不会快速幂戳这里： http://www.cnblogs.com/hadilo/p/5719139.html ），那么矩阵一样也是可以的是不是

　　因为对于方阵A来说，(A2)2=A4

　　于是实数怎样做快速幂，矩阵就怎样做

1 while (m>0)
2     {
3         if (m%2) mult(b,a);
4         m/=2;
5         mult(a,a);
6     }

 

　　手写一个 mult 函数，就用最普通的 n3 矩阵乘法

　 （矩阵的基本运算，通俗易懂 http://www.cnblogs.com/hadilo/p/5865541.html）

 1 void mult(int x[N][N],int y[N][N])
 2 {
 3     int i,j,k;
 4     for (i=1;i<=n;i++)
 5         for (j=1;j<=n;j++)
 6             {
 7                 c[i][j]=0;
 8                 for (k=1;k<=n;k++) c[i][j]=(c[i][j]+x[i][k]*y[k][j])%mo;
 9             }
10     for (i=1;i<=n;i++)
11         for (j=1;j<=n;j++) x[i][j]=c[i][j];
12 }

 

　　但题目要求的是 A+A2+...+Ak，而不是单个矩阵的幂

　　那么我们可以构造一个分块的辅助矩阵 S，其中 A 为原矩阵，E 为单位矩阵，O 为0矩阵

　　

　　我们将 S 取幂，会发现一个特性

　　

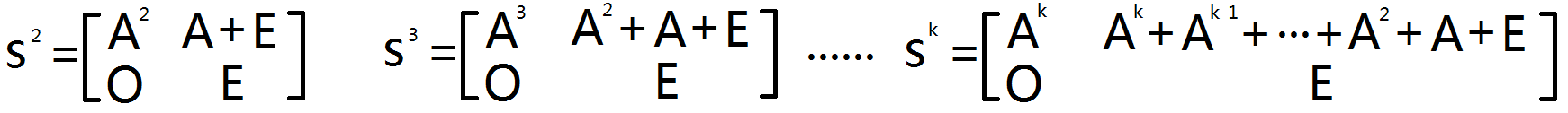
　　Sk 右上角那一块不正是我们要求的 A+A2+...+Ak 吗？

　　于是我们构造出 S 矩阵，然后对它求矩阵快速幂即可，最后别忘了减去一个单位阵

　　时间降为O(n3log2k)，从一个月到0.8秒的跨越

 1 #include<algorithm>
 2 #include<iostream>
 3 #include<cstdlib>
 4 #include<cstring>
 5 #include<cstdio>
 6 #include<cmath>
 7 using namespace std;
 8 
 9 const int N=61;
10 int c[N][N],a[N][N],b[N][N],n,mo;
11 void mult(int x[N][N],int y[N][N])
12 {
13     int i,j,k;
14     for (i=1;i<=n;i++)
15         for (j=1;j<=n;j++)
16             {
17                 c[i][j]=0;
18                 for (k=1;k<=n;k++) c[i][j]=(c[i][j]+x[i][k]*y[k][j])%mo;
19             }
20     for (i=1;i<=n;i++)
21         for (j=1;j<=n;j++) x[i][j]=c[i][j];
22 }
23 int main()
24 {
25     int m,i,j;
26     scanf("%d%d%d",&n,&m,&mo);
27     for (i=1;i<=n;i++)
28         {
29             for (j=1;j<=n;j++) scanf("%d",&a[i][j]);
30             a[i][i+n]=a[i+n][i+n]=b[i][i]=b[i+n][i+n]=1;
31         }
32     n*=2;
33     m++;
34     while (m>0)
35         {
36             if (m%2) mult(b,a);
37             m/=2;
38             mult(a,a);
39         }
40     n/=2;
41     for (i=1;i<=n;i++) b[i][i+n]--;
42     for (i=1;i<=n;i++)
43         {
44             for (j=1;j<n;j++) printf("%d ",b[i][j+n]);
45             printf("%d\n",b[i][j+n]);
46         }
47     return 0;
48 }

 

 

 

版权所有，转载请联系作者，违者必究

QQ：740929894

posted @ 2016-09-24 16:32  Hadilo  阅读(3533)  评论(7)  编辑  收藏  举报