求LCA最近公共祖先的在线ST算法_C++

　　ST算法是求最近公共祖先的一种 在线 算法，基于RMQ算法，本代码用双链树存树

　　预处理的时间复杂度是 O(nlog2n)   查询时间是 O(1) 的

　　另附上离线算法 Tarjan 的链接：

　　　　http://www.cnblogs.com/hadilo/p/5840390.html

 

 

　　首先预处理出深度，以及 DFS 序，这里的DFS序是指回溯时也算上，比如

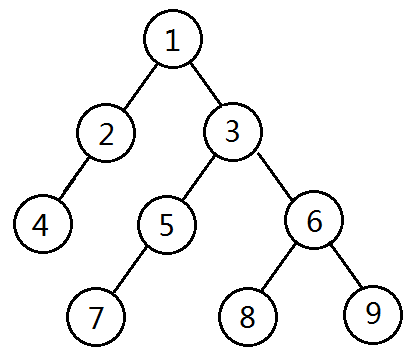
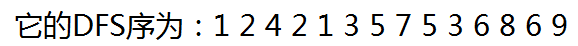
 1 void dfs(int x,int dep)
 2 {
 3     int i;
 4     d[x]=dep;
 5     a[++top]=x;
 6     for (i=down[x];i!=0;i=next[i])
 7     {
 8         dfs(i,dep+1);
 9         a[++top]=x;
10     }
11 }

　　然后记录每个节点在 DFS 序中第一次出现的位置，b[i] 为第 i 号节点第一次出现的位置

1     for (i=1;i<=top;i++) if (b[a[i]]==0) b[a[i]]=i;

 

 

　　开始 DP 处理区间区间内最小值，这里使用 RMQ 算法，其功能类似于线段树或树状数组

　　f[i][j] 表示从第 i 位开始，连续 2j 个数的最小值，状态转移：

1     f[i][j]=min(f[i][j-1],f[i+(1<<(j-1))][j-1])

　　因为它是 2 的幂次方的状态，所以每次转移可以看做把当前状态分为两个相等的部分，求两部分的最小值

　　如： 5 7 3 2   和   4 6 1 5

　　　　 min=2           min=1

  　即 f[1][2]=2       f[5][2]=1

　　所以 f[1][3]=min(f[1][2],f[5][2])=1

　　初始状态：f[i][0]=d[a[i]]    loc[i][0]=a[i]

　　注意这里 f 记录的是它的深度的最小值，而位置用 loc 记录

 1 void init()
 2 {
 3     int i,j,s,x,k;
 4     for (i=1;i<=top;i++)
 5     {
 6         f[i][0]=d[a[i]];
 7         loc[i][0]=a[i];
 8     }
 9     s=log2(top);
10     for (j=1;j<=s;j++)
11     {
12         k=top-(1<<j)+1;
13         for (i=1;i<=k;i++)
14         {
15             x=i+(1<<(j-1));
16             if (f[i][j-1]<=f[x][j-1])
17             {
18                 f[i][j]=f[i][j-1];
19                 loc[i][j]=loc[i][j-1];
20             }
21             else
22             {
23                 f[i][j]=f[x][j-1];
24                 loc[i][j]=loc[x][j-1];
25             }
26         }
27     }
28 }

　　代码用变量优化了一下常数

　　接着开始进行询问

　　读入两个节点，查询它们第一次出现的位置

　　在这两个位置之间的区间查询最小深度的节点，该节点即为最近公共祖先

　　查询区间时，我们把它分成两个部分，可以有重叠，如

　　　　8 9 6 5 6 8 4

　　这7个节点，把它分成： 8 9 6 5  和 5 6 8 4

　　　　　　　　　　　　　 min=5      min=4

　　则最小值为 min(5,4)=4

1     min(f[x][log2(y-x)],f[y-(1<<i)+1][log2(y-x)]);

　　可以这样理解：

　　　　将两个位置的距离取个对数记为 i，然后从最左边，往后共 2i 个数的最小值，这是第一部分

　　　　第二个部分是从右边往左推 2i 个数，即 y-2i+1，然后再往后取 2i 个数

　　成功将区间分为两部分

 1     scanf("%d",&t);
 2     while (t>0)
 3     {
 4         t--;
 5         scanf("%d%d",&x,&y);
 6         x=b[x];
 7         y=b[y];
 8         if (x>y) swap(x,y);
 9         i=log2(y-x);
10         k=y-(1<<i)+1;
11         printf("%d\n",f[x][i]<f[k][i]?loc[x][i]:loc[k][i]);
12     }

 

 

　　代码内有常数优化，有的地方思路可能不是很清晰，请谅解

　　给个完整代码

 1 #include<cstdio>
 2 #include<cstdlib>
 3 #include<cstring>
 4 #include<cmath>
 5 #include<iostream>
 6 #include<algorithm>
 7 #define N 100001
 8 using namespace std;
 9 
10 int a[N*2],d[N],down[N],next[N],top,f[2*N][18],loc[2*N][18],n,b[N];
11 int log2(int x)
12 {
13     int k=0;
14     while (x>1)
15     {
16         x/=2;
17         k++;
18     }
19     return k;
20 }
21 void dfs(int x,int dep)
22 {
23     int i;
24     d[x]=dep;
25     a[++top]=x;
26     for (i=down[x];i!=0;i=next[i])
27     {
28         dfs(i,dep+1);
29         a[++top]=x;
30     }
31 }
32 void init()
33 {
34     int i,j,s,x,k;
35     for (i=1;i<=top;i++)
36     {
37         f[i][0]=d[a[i]];
38         loc[i][0]=a[i];
39     }
40     s=log2(top);
41     for (j=1;j<=s;j++)
42     {
43         k=top-(1<<j)+1;
44         for (i=1;i<=k;i++)
45         {
46             x=i+(1<<(j-1));
47             if (f[i][j-1]<=f[x][j-1])
48             {
49                 f[i][j]=f[i][j-1];
50                 loc[i][j]=loc[i][j-1];
51             }
52             else
53             {
54                 f[i][j]=f[x][j-1];
55                 loc[i][j]=loc[x][j-1];
56             }
57         }
58     }
59 }
60 int main()
61 {
62     int i,k,x,y,t;
63     scanf("%d",&n);
64     for (i=1;i<=n;i++) down[i]=d[i]=next[i]=0;
65     for (i=1;i<=n;i++)
66     {
67         scanf("%d",&x);
68         next[i]=down[x];
69         down[x]=i;
70     }
71     top=0;
72     dfs(down[0],1);
73     for (i=1;i<=top;i++) if (b[a[i]]==0) b[a[i]]=i;
74     init();
75     scanf("%d",&t);
76     while (t>0)
77     {
78         t--;
79         scanf("%d%d",&x,&y);
80         x=b[x];
81         y=b[y];
82         if (x>y) swap(x,y);
83         i=log2(y-x);
84         k=y-(1<<i)+1;
85         printf("%d\n",f[x][i]<f[k][i]?loc[x][i]:loc[k][i]);
86     }
87     return 0;
88 }

 

 

 

版权所有，转载请联系作者，违者必究

QQ：740929894

posted @ 2016-09-03 16:57  Hadilo  阅读(3054)  评论(0)  编辑  收藏  举报