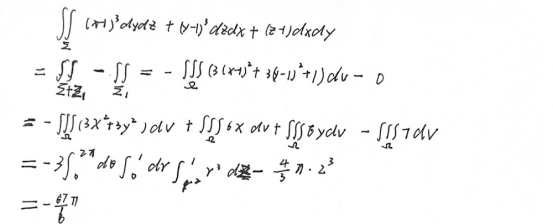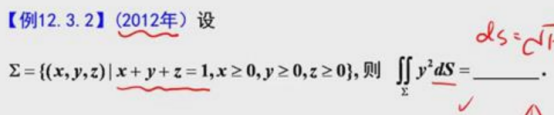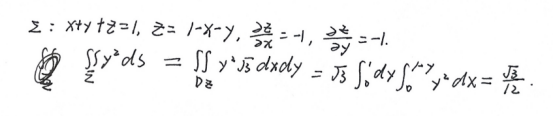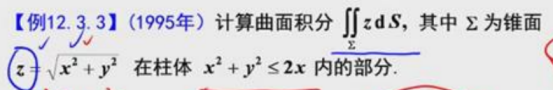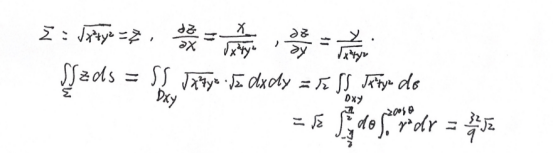曲面积分计算

一、一型曲面积分

一型曲面积分共有三种计算方法，且不需考虑正负的问题。以直角计算为主，奇偶性、对称性为辅助。

（一）直接计算法——直角坐标下

因为是在曲面上进行积分，所以曲面方程Z=Z(x, y)可以直接带入方程中。带入后消去了z，曲面积分转变成了在D（曲面在xoy上的投影）上的二重积分。

由于

 

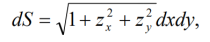
 故积分表达式可化为

 

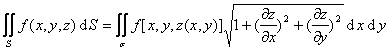
 能把曲线/曲面方程带入积分函数计算的只有两种：曲线积分、曲面积分。

不能代入计算的是：重积分

（二）利用奇偶性

被积函数若是关于x的奇函数，且积分曲面关于yoz前后对称，那么该积分等于0；

若被积函数若是关于x的偶函数，且积分曲面关于yoz前后对称，那么该积分等于二倍的对yoz前边曲面上的积分。

若对于y、z也有奇偶性，同理。

（三）利用对称性（轮换性）

若积分曲面x，y，z位置可以对调，积分函数内x，y，z也可以互换，最后积分结果不变。

二、二型曲面积分

二型曲面积分共有三种计算方式。因为二型曲面积分是对曲面上dx和dy做的投影，存在正负号的问题。所以二型曲面积分必须考虑积分正负号的问题。

二型曲面积分与在曲面哪一侧积分有关：

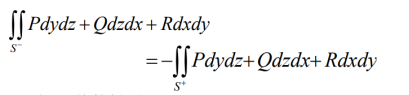
（一）直接计算法

 设曲面：z=z(x, y)，曲面对xoy投影D。

把z=z(x, y)带入积分计算，于是转化成二重积分。

 

（二）高斯公式

 若曲面封闭可以用高斯公式，将二型曲面积分转化成三重积分。

一定要注意正负号的问题。

 

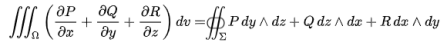
 PS 如何判断正负号呢？

看题设，题目一般指输出哪一侧（内侧，外侧）为正。

（三）补面后再利用高斯公式

类似于格林公式补线，但需要注意的是，补完后形成的封闭曲面用高斯公式计算积分的时候要注意正负号，还要记得减去新添加的面的积分。给这个新添加的曲面计算积分时，同样要注意正负号。

三、下面是例题