三重积分计算

核心思想：化成定积分或二重积分

注意应用三重积分的性质：

奇偶性：看积分函数。若积分函数是关于x的奇函数，且积分空间关于zoy对称，那么该积分等于0；若积分函数是关于x的偶函数，且积分空间关于zoy对称，那么该积分就等于2倍的积分空间（x>0）上的积分；

轮换性：看积分空间，若x和y和z可以任意交换次序，积分函数可以更换成易于积分的形式。

一、直角法

（一）先一后二

先单积分，后重积分。

 

Dxy：积分空间对xoy平面的投影

Z(x,y)：积分曲面上下界

（二）先二后一

先重积分，后单积分。

 

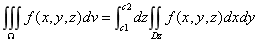
Dz：用z=z去截积分空间得到的平面

• 何时用？

若被积函数是关于z的一元函数，首选该方法。

或者用z去截得到的面积好求，也采用该方法。

二、柱坐标法

 

 

 

 

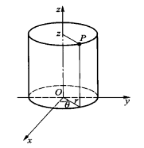
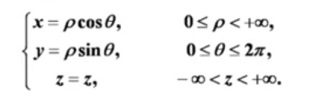
• 何时用？

从被积函数看：

被积函数是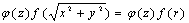的形式。

从积分空间看：

柱体、锥体

三、球面坐标法

 

 

 

 

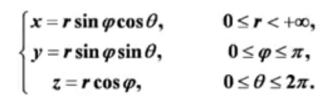
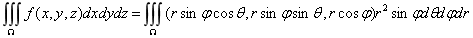
•  何时用？

从积分函数看，含有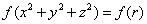

从积分区域看，含有球、部分球、锥体、部分锥体

四、例题

（一）

解法如下：

因为x是关于x的奇函数，而且积分空间关于yoz对称，故关于x的积分等于0；只需要计算对z的积分。下面列举几个方法：

 

（二）

因为积分区间为球体，故选择球坐标进行计算。