数据结构（Data Structure）的基本思想是增删改查
本文主要观点
- 在Data Structure中，Data（数据）是我们要处理的事物，Structure（结构）是辅助我们处理数据的工具。
- 数据结构中的“结构”，具有对“数据”进行四种增、删、改、查四种基本的操作，其他的高级操作都是这四种基本操作的变形与综合。
数据结构（Data Structure）的基本定义
- Data：你要存储和表示的事物。例如，你要存储一个班的所有同学的年龄，这个年龄就是数据。
- Structure：数据要如何组织、如何存储磁盘。例如，使用一个数组存储一个班的年龄，这些年龄顺序地存储在一块连续的内存空间里。其中数组被称为逻辑结构，存储于一块连续的内存空间被称为物理结构。
本文要求读者有一定的“数据结构基础知识”，可能不适合初学者阅读！
内容导览
数据的逻辑结构
“物理”与“逻辑”是计算机科学中常用的一对概念，理解它可以帮助我们学习得更快！
物理：真实存在的事物；虚拟：根据真实的事物虚拟、假定出的概念。
例如：你间隔很多天下载一部电影放在电脑上的某文件夹内。在逻辑上，这些电影都放在一个文件夹内，对你来说，你打开这个文件夹，就能找到这些电影；然而在物理上，他们极可能不是紧挨着存储于磁盘上的，可能第一部电影存储于1号盘面的扇区20，第二部电影存储于3号盘面的扇区50。
数据的逻辑结构，也就是数据的组合方式
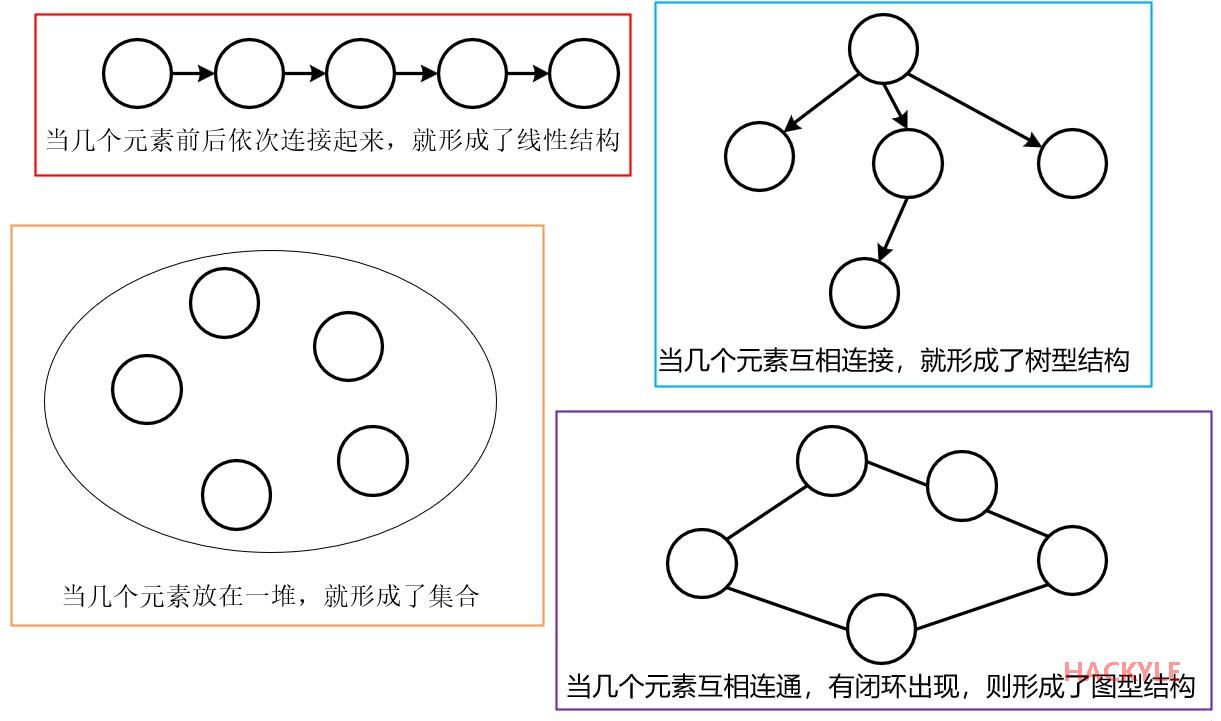
- 线性结构
- 数据元素之间只存在一对一的关系
- 例如数组，第1个元素与第二个元素只存在一对一的关系。
- 集合结构
- 数据元素之间除了“同属于一个集合”的关系外，别无其他关系。
- 例如，Java集合中的Set类型，集合内的元素保持唯一性、无序性。
- 树形结构
- 数据元素之间存在一对多的关系。
- 例如二叉树，一个节点，可以有2个子节点和1个父节点。
- 图状结构
- 数据元素之间存在多对多的关系。
- 例如无向图，一个节点有多个相邻节点，每个相邻节点也可以有多个相邻节点。
数据的存储结构
存储结构表明数据在计算机的内存中是如何被存储的，在计算机内存中的表示（又称映像），也称物理结构
顺序存储
- 把逻辑上相邻的元素存储在物理位置上也相邻的存储单元里，元素之间的关系由存储单元的邻接关系来体现。
- 优点：可以实现随机存取，每个元素占用最少的存储空间；
- 缺点：只能使用相邻的一整块存储单元，因此可能产生较多的外部碎片。
- 例如：数组
链式存储
- 用指针表示元素之间的逻辑关系。
- 优点：不会出现碎片现象，充分利用所有存储单元；
- 缺点：每个元素因存储指针而占用额外的存储空间，并且只能实现顺序存取。
- 例如：单链表
索引存储
- 在存储元素信息的同时，还建立附加的索引表。索引表中的每一项称为索引项，索引项的一般形式是：（关键字，索引地址）。
- 优点：检索（查询）速度快；
- 缺点：增加了附加的索引表，会占用较多的存储空间。另外，在增加和删除数据时要修改索引表，因而会花费较多的时间。
- 例如：MySQL中为某些字段建立索引
散列存储
- 根据元素的关键字直接计算出该元素的存储地址，又称为Hash存储。
- 优点：检索、增加和删除结点的操作都很快；
- 缺点：如果散列函数不好可能出现元素存储单元的冲突，而解决冲突会增加时间和空间开销。
- 例如：Java中的HashMap
数据的运算
在Data Structure中，Data（数据）是我们要处理的事物，Structure（结构）是辅助我们处理数据的工具。
还是以一个数组来表示一个班的年龄为例。
- 班级里新来了一个同学，年龄如何存储到数组中呢？数组的插入
- 班级里离开了一个同学（转校），如何删除？数组的删除
- 一个年龄录入错了，如何修改？数组的修改
- 如何获取某位同学的年龄？数组的查询
其中的“插入”、“删除”、“修改”、“查询”就是【数组】这种数据结构的基本运算。我们可以通过这些基本运算实现我们想要的功能。
数据运算的例子
- 运算例子1：班级同学平均年龄？对数组求和，再除以数组元素的个数
- 运算例子2：班级同学年龄的最大、最小？对数组进行最值查找
所以，我们用“抽象数据类型(Abstract Data Type)”更规范化地表达数据的结构，以及对数据的操作
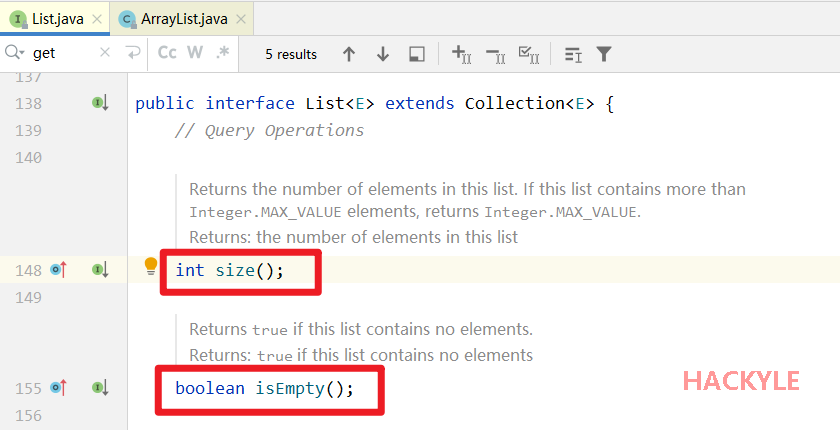
以Java为例，上图中的红色框内就是一种抽象数据类型，它定义了一种对数据的操作
数据的增删改查
在数据库中，还是对于表中的记录，有四种基本的操作：增删改查，其他的操作都是这四种基本操作的变形或是综合。
将这种思想引入到数据结构中：数据结构中的“结构”，具有对“数据”进行四种增、删、改、查四种基本的操作，其他的高级操作都是这四种基本操作的变形与综合。其中，“增”的含义是：创建、插入、新增，“删”的含义是：删除元素，“改”的含义是：修改，“查”的含义是：查找，查询。
例如：在一个数组（一种线性顺序表）中，在指定的下标中插入元素涉及到的操作有：查找，移动（修改），插入，有三种基本操作。
于是，学习任意一种数据结构，只要牢牢把握住这种“结构”的增删改查四种基本操作，其他的操作都是四种基本数据类型的变形与综合！
