顺序表的基本操作与重要思想

本文的主要内容是高度总结顺序表的两种具体模型（线性顺序表、链式顺序表）的基本操作和一般操作套路。

什么是基本操作？

根据这篇文章（数据结构（Data Structure）的基本思想是增删改查）中提出的观点：数据结构中的“结构”，具有对“数据”进行四种增、删、改、查四种基本的操作，其他的高级操作都是这四种基本操作的变形与综合。
其中，“增”的含义是：创建、插入、新增，“删”的含义是：删除元素，“改”的含义是：修改，“查”的含义是：查找，查询。
所以，对顺序表的基本操作就是对元素的增、删、改、查。

什么是一般操作套路？

顺序线性表的本质就是数组。操作数组的套路有双下标思想、快慢下标思想等。
链式顺序表。操作链表的套路有快慢指针、辅助链表思想等。

线性表？顺序表？

线性表是一种逻辑结构，表示元素之间一对一的相邻关系。顺序表和链表是指存储结构。
也即线性表表明数据之间的逻辑结构是线性的；顺序表和链表表明数据的存储结构是顺序的。

本文中所有的实现代码：https://github.com/HackyleShawe/DataStructure/tree/master/01-LinearList

内容导览

线性顺序表(数组)
- 基本操作
  - Create
  - Delete
  - Update
- 基本思想
链式顺序表

线性顺序表(数组)

顺序表的本质就是：数组！顺序表等价于数组！

理解顺序存储结构：

是四大存储结构中的一种（顺序存储、链式存储、索引存储、散列存储）；
定义：把逻辑上相邻的结点存储在物理位置上相邻的存储单元中，结点之间的逻辑关系由存储单元的邻接关系来体现。
理解：具有线性关系的数据、按照前后的次序、全部存储在一整块连续的内存空间中，即用一组地址连续的存储单元、依次存储线性表的各个数据元素

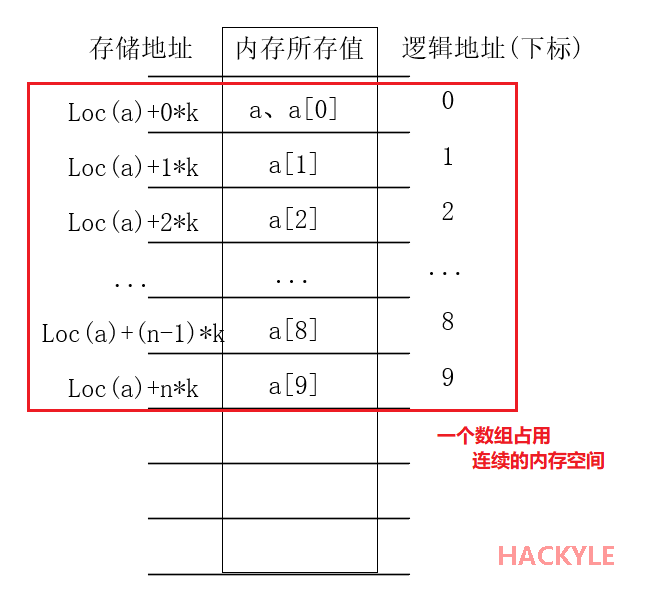
如果一个数组为”a[10]={11,12,13,14,15,16,17,18,19.20}”。存储的是int型数据，所以该数组是int型数组，所以k的值为int型数据的宽度（即为4字节）。

顺序存储的特性：

第一个元素所在的地址就是这块存储空间的首地址。通过首地址，可以轻松访问到存储的所有的数据。
可实现对结点的随机存取，即每一个结点对应一个序号，由该序号可以直接计算出来结点的存储地址。

顺序表的定义：

#define SIZE 100   //存储空间初始分配量
typedef struct Sqlist
{
	int element[SIZE];   //数组存储数据元素，最大长度为SIZE
	int current;     //线性表当前长度
}Sqlist, * PSqlist;

注：为了简便化，后续的使用中直接使用数组替代顺序表。在我的文章中，如无特殊说明，数组即代表顺序表！

基本操作

在数据库中，还是对于表中的记录，有四种基本的操作：增删改查，其他的操作都是这四种基本操作的变形或是综合。

将这种思想引入到数据结构中：数据结构中的“结构”，具有对“数据”进行四种增、删、改、查四种基本的操作，其他的高级操作都是这四种基本操作的变形与综合。其中，“增”的含义是：创建、插入、新增，“删”的含义是：删除元素，“改”的含义是：修改，“查”的含义是：查找，查询。

例如：在一个数组（一种线性顺序表）中，在指定的下标中插入元素涉及到的操作有：查找，移动（修改），插入，有三种基本操作。

于是，学习任意一种数据结构，只要牢牢把握住这种“结构”的增删改查四种基本操作，其他的操作都是四种基本数据类型的变形与综合！

引用：https://blog.hackyle.com/article/datastructure/the-basic-thought-is-crud

Create

合并两个有序的数组为一个

同时遍历两个有序数组，将符合条件的下标前进，不符合条件的下标不动；
看那个数组还有剩余，将剩余的依次顺序加入到新的数组即可；

Delete

删除数组中所有的指定值

朴素算法：遍历数组，遇到X，将其后面的元素全部向前挪一位。
从头开始的双下标思想：设定：i遍历数组，k为符合条件的数组下标；当元素不等于指定值时，将下标i的值赋值给下标k。

删除无序表中元素值在区间[X, Y]内的元素

双下标思想。设定：i遍历数组，k为符合条件的数组下标
当Arr[i]不等于区间[X, Y]内的元素时，将下标i的值赋值给下标k

删除有序表中元素值在区间[X, Y]内的元素

双下标思想
- 遍历数组，找到最后一个小于X的下标为k
- 继续遍历，从第一个大于Y的下标i开始，a[k++] = a[i]

删除有序数组中的重复值

分析：值相同的元素一定在连续的位置上
算法：
- 遍历时，判断当前元素a[i](i>=1)与前一个元素a[i-1]是否相同
- 如果相同，则continue。这一步就跳过了那些相同的元素
- 如果不相同，则a[k++] = a[i], i>=1

Update

就地逆置-前后颠倒

需求：将数组的所有元素前后颠倒，要求时间复杂度为O(n)，空间复杂度为O(1)
算法：遍历前半部分，把第i个数与第n-i-1个数交换

部分元素互换

一个数组a，长度为len。将下标为[0, k]与下标为[k+1,len-1]之间的元素交换。
例如，数组a[6]={1,2,3,4,5,6}，将前三个与后三个交换后，a[6]={4,5,6,1,2,3};

算法A：收集下标[0, k]于临时数组X，收集下标为[k+1,len-1]为临时数组Y，按先Y后X拼接数组

算法B：将数组就地逆置，再将[0,k]与[k+1,len-1]之间的元素就地逆置。

按大小划分为两个部分

需求：给定一个数组arr，和一个数num，请把小于等于num的数放在数组的左边，大于num的数放在数组的右边。要求额外空间复杂度O(1)，时间复杂度O(N)。

算法思想：从头开始的双下标思想

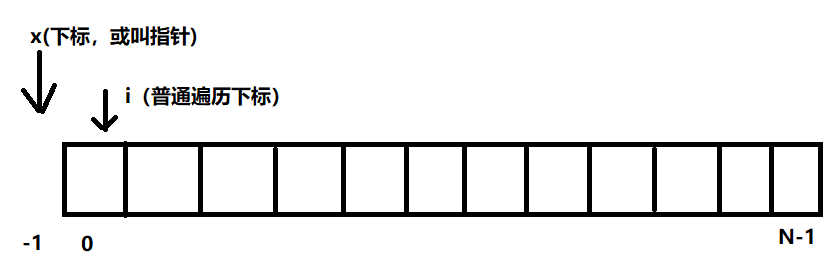
下标x的含义是：下标为0~x之间的数全部是小于等于num的，也就是该区域、范围里的数是小于等于num的；初始时x的值为-1，表示还不存在有小于等于num的范围。
遍历：如果遇到a[i]≤num，则把a[i]和上述区域内的最后一个值交换，然后再扩大上述区域；如果遇到a[i]>num，直接跳到下一个位置，即i++；

实现代码：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>

void exchange(int* a, int len, int num)
{
	int i; //遍历使用的下标
	int x; //[0,x]区域内的所有数都小于等于num
	int t; //交换两个数时使用的临时变量

	x = 0;//x = -1; //初始时小于等于num的区域不存在
	for (i = 0; i < len; i++)
	{
		if (a[i] < num)
		{
			t = a[i]; a[i] = a[x]; a[x] = t;
			x += 1; //属于小于等于num的区域扩大
		}
	}
}

int main()
{
	int len = 5;
	int num = 5;
	int i;

	scanf("%d", &len);
	int* a = (int*)malloc(sizeof(int) * len);
	for (i = 0; i < len; i++)
	{
		scanf("%d", &a[i]);
	}
	scanf("%d", &num);

	exchange(a, len, num);
	for (i = 0; i < len; i++)
	{
		printf("%d ", a[i]);
	}

	return 0;
}

荷兰国旗问题

需求：给定一个数组arr，和一个数num，请把小于num的数放在数组的左边，等于num的数放在数组的中间，大于num的数放在数组的右边。要求额外空间复杂度O(1)，时间复杂度O(N)

算法思想：（三下标思想）

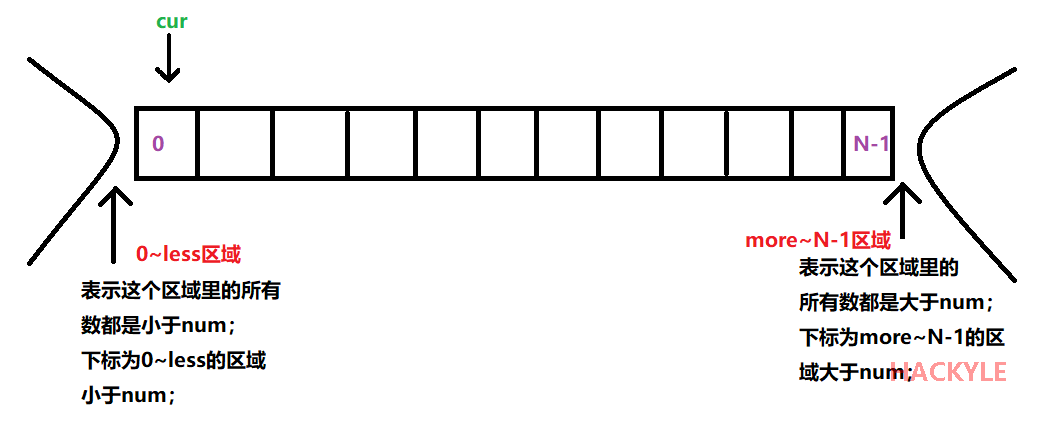
遍历过程中：

如果发现a[cur]小于num，则直接把a[i]与[0, less]区域里的最后一个数交换，然后less++，cur++（也就是小于num的区域内地数增加，又继续看下一个数）；
如果a[cur]等于，num，则什么都不做，直接看下一个；
如果a[cur]>num，则把a[cur]和[more, N-1]区域的第一个数交换，然后，more--（也就是more向前扩一个位置）；然后看缓过来的那个数，是等于num的？还是小于num的？再执行“①②”中所提到的操作；
当cur等于more相等的时候，表示停止操作。

实现代码：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>

void NetherlandsFlag(int* a, int L, int R, int num)
{
	int less = L - 1;
	int more = R + 1;
	int cur = L;
	int t;

	while (cur < more)
	{
		if (a[cur] < num) //对应算法思想中的①操作
		{
			less++; //因为初始时less=L-1，当L=0时，less=-1；若不先加一，则a[-1]不合法！
			t = a[less]; a[less] = a[cur]; a[cur] = t;
			cur++;
		}
		else if (a[cur] > num) //对应算法思想中的③操作
		{
			more--;
			t = a[cur]; a[cur] = a[more]; a[more] = t;
		}
		else  //对应算法思想中的②操作
		{
			cur++;
		}
	}
	//最终的等于区域是：下标为[less+1, more-1]
}

int main()
{
	int len = 5;
	int num = 5;
	int i;

	scanf("%d", &len);
	int* a = (int*)malloc(sizeof(int) * len);
	for (i = 0; i < len; i++)
	{
		scanf("%d", &a[i]);
	}
	scanf("%d", &num);

	NetherlandsFlag(a, 0, len-1, num);
	for (i = 0; i < len; i++)
	{
		printf("%d ", a[i]);
	}

	return 0;
}

基本思想

请重新看上文中提到的相关例子，在具体的例子中体会数组的操作思想（一般套路）！

双下标思想

从两端向中间的双下标
从头开始的双下标（快慢双下标）
例如：数组Partition问题

三下标思想

例如：荷兰国旗问题

链式顺序表

理解链式存储结构

是四大存储结构中的一种（顺序存储、链式存储、索引存储、散列存储）；
定义：用一组地址任意的存储单元存放各个数据元素。
理解：区别于顺序存储结构，所有的数据元素不是存储在一块连续的存储空间上，而是存储在任意内存单元上。

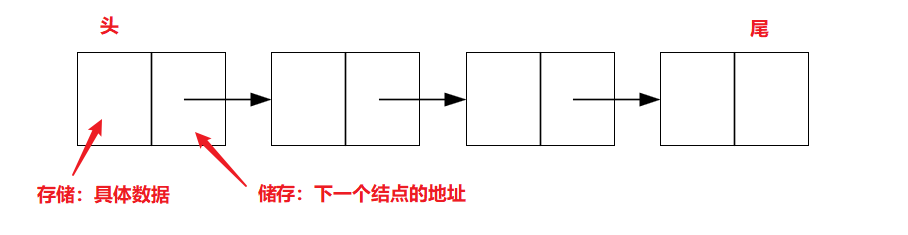
链表初识

链表是一种链式存取的数据结构，用一组地址任意的存储单元存放线性表中的数据元素和下一元素的地址。
链表中的数据是以结点来表示的，每个结点的构成：元素 + 指针(下一元素的存储位置)。元素就是存储数据的存储单元，指针就是连接每个结点的地址数据。

单链

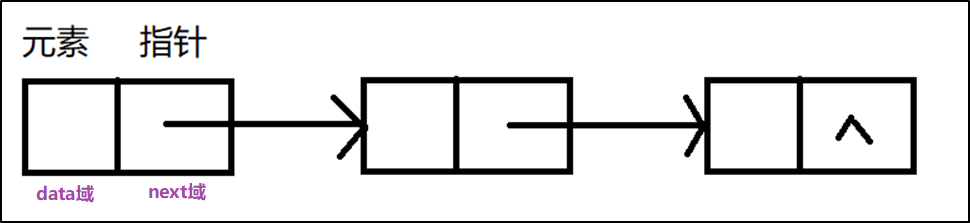
定义：链表通过每个结点的链域将线性表的n个结点按其逻辑顺序链接在一起的，每个结点只有一个链域的链表称为单链表（Single Linked List）。

单链表特性：

物理上不连续，逻辑上连续：可以将物理地址上不连续的内存空间连接起来，通过指针来对物理地址进行操作，实现逻辑上的连续（线性）。
头指针：单链表中每个结点的存储地址是存放在其前趋结点的next域中，而开始结点无前趋，故应设头指针head指向开始结点。链表由头指针唯一确定。
尾巴：终端结点无后继，故终端结点的指针域为空，即NULL。

单链表节点定义

typedef struct node
{
	int data;
	struct node* next;
}Node;

两种分类：带头结点的单链表和不带头头结点的单链表

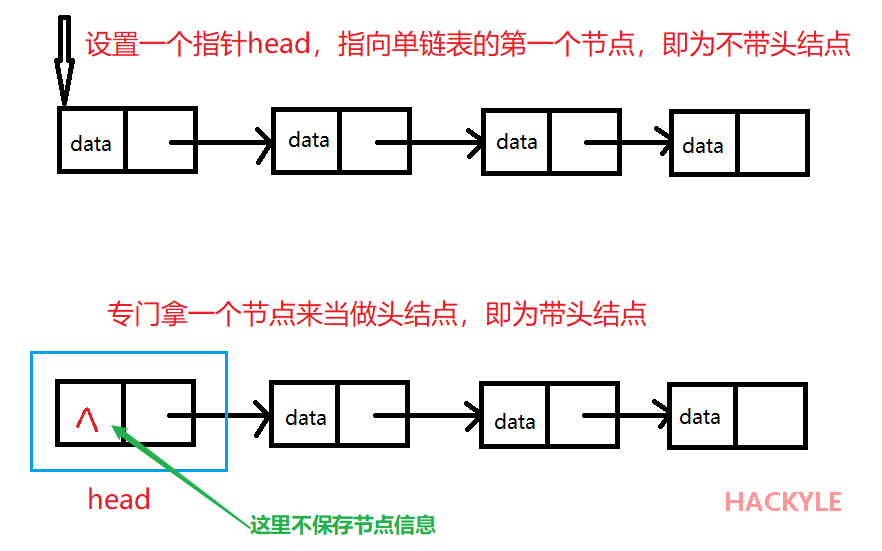
不带头结点的单链表：也就是 head 只是一个指针，指向链表的第一个节点。
带头结点的单链表：头结点的data不保存信息，next指针指向链表的第一个具有data域结点。

第一个单链表程序

#include <stdio.h>
#include <malloc.h>
#include <assert.h>

typedef struct node
{
	int data;
	struct node* next;
}Node; //struct node 完全等于 Node（结构体变量）
typedef Node* LinkList; //struct node * 完全等于 LinkList（结构体指针）

int main()
{
	LinkList head = (LinkList)malloc(sizeof(Node));
	assert(head != NULL);  //检查malloc之后是不是空间不够，返回了空指针NULL（WarningC6011：取消对NULL指针的引用）
	LinkList NodeAa = (LinkList)malloc(sizeof(Node));
	assert(NodeAa != NULL);
	LinkList NodeBb = (LinkList)malloc(sizeof(Node));
	assert(NodeBb != NULL);
	LinkList NodeCc = (LinkList)malloc(sizeof(Node));
	assert(NodeCc != NULL);

	head->data = 101;
	head->next = NodeAa;
	NodeAa->data = 202;
	NodeAa->next = NodeBb;
	NodeBb->data = 303;
	NodeBb->next = NodeCc;
	NodeCc->data = 404;
	NodeCc->next = NULL;

	LinkList p = head; //把链表的头结点交给指针p，去遍历
	while (p != NULL)
	{
		printf("%d  ", p->data);
		p = p->next;
	}
	return 0;
}

Create

头插法创建单链表

尾插法创建

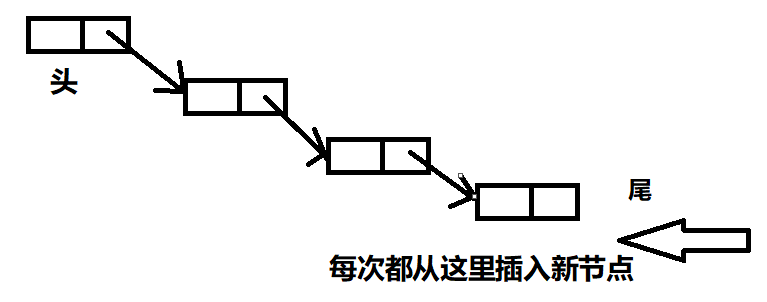
插入新元素

后插：

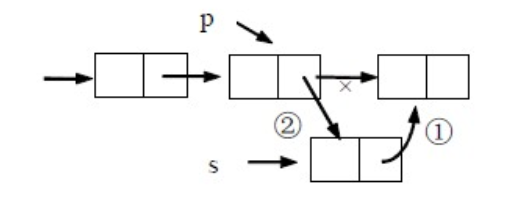
*p之后插入*s

①s->next=p->next;
②p->next=s;
//注意：两个指针的操作顺序不能交换。

前插算法一（本质上还是后插）：

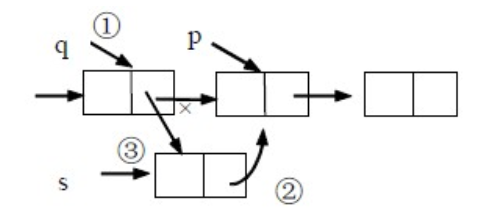
*p之前插入*s
找到其要插入的位置（*p）的前一个节点（*q），在*q执行后插操作；

前插算法二（本质上还是后插）：

设待插入的节点为*s，要实现将*s插入到*p的前面。我们任然将*s插入到*p的后面，然后将p->data于s-。
data交换，这样既满足了逻辑关系，又能使得时间复杂度为O(1)。

Delete

删除方式一：找其前驱、后驱，连接前后驱即可实现删除

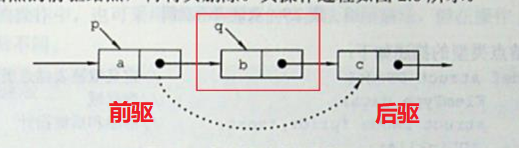
删除方式二：将后驱节点的值取出，放到当前节点，删除后驱节点。

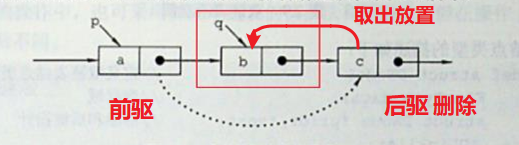
去除重复元素：算法思想类似于数组，快慢指针

Update

就地逆置

需求：单链表的就地逆置，实现的效果如下图：

算法：将原链表的元素逐个取下，利用头插法重新连接起来。

元素条件划分

需求：将单向链表按某值划分成左边小、中间相等、右边大的形式。

详细描述

给定一个单向链表的头节点head，节点的值类型是整型，再给定一个整数pivot。
实现一个调整链表的函数，将链表调整为左部分都是值小于pivot的节点，中间部分都是值等于pivot的节点，右部分都是值大于 pivot的节点。
除这个要求外，对调整后的节点顺序没有更多的要求。例如：链表9->0->4->5->1，pivot=3。调整后链表可以是1->0->4->9->5，也可以是0->1->9->5->4。
总之，满足左部分都是小于3的节点，中间部分都是等于3的节点（本例中这个部分为空），右部分都是大于3的节点即可。对某部分内部的节点顺序不做要求。

算法思想

辅助空间思想1：直接整个链表复制到一个数组中，直接使用荷兰国旗思想。
辅助空间思想2：设置三个队列（或其他容器），遍历符合条件的放入队列中，遍历完毕后，一次输出三个队列即可。

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
using namespace std;
typedef struct node
{
	int data;
	struct node* next;
}list;

list* CreateList(int n)
{
	if (n == 0)
	{
		return NULL;
	}
	int i;
	int t;
	list* head=NULL;
	list* move =NULL;
	list* new_node;
	for (i = 0; i < n; i++)
	{
		scanf("%d", &t);
		new_node = new list;
		new_node->data = t;
		new_node->next = NULL;

		if (head == NULL)
		{
			head = new_node;
			move = head;
		}
		else
		{
			move->next = new_node;
			move = move->next;
		}
	}
	return head;
}
void ShowList(list* head)
{
	while (head != NULL)
	{
		cout << head->data << " ";
		head = head->next;
	}
	cout << endl;
}

void swap(vector<int>& ve, int i, int j)
{
	int tmp = ve.at(i);
	ve.at(i) = ve.at(j);
	ve.at(j) = tmp;
}
void NetherlandsFlag(vector<int> &ve, int pivot)
{
	int small = -1; //区域(0,small]是小于pivot的元素下标
	int big = ve.size() - 1; //区域[big,ve.size()-1]是大于pivot的元素下标
	int i=0; //循环下标
	while (i != big)
	{
		if (ve.at(i) < pivot)
		{
			swap(ve, ++small, i++);
		}
		else if (ve.at(i) == pivot)
		{
			i++;
		}
		else
		{
			swap(ve, --big, i);
		}
	}
}
void ListPartition(list* head, int pivot)
{
	if (head == NULL)
	{
		return;
	}
	list* cur = head;
	vector<int> ve;

	while (cur != NULL)//把链表中的元素拷贝到数组中，再利用荷兰国旗思想解决问题
	{
		ve.push_back(cur->data);
		cur = cur->next;
	}
	NetherlandsFlag(ve,pivot);
	cur = head;
	for (vector<int>::iterator it = ve.begin(); it != ve.end(); *it++) //把经过荷兰国旗处理了的又拷贝回链表
	{
		cur->data = *it;
		cur = cur->next;
	}
}

void test01()
{
	int n = 5;
	list* my_list = NULL;
	my_list = CreateList(n);
	ShowList(my_list);
	ListPartition(my_list, 5); //条件划分处理
	ShowList(my_list);
}
int main()
{
	test01();
	return 0;
}

元素划分问题进阶

在原问题的要求之上再增加如下两个要求。

在左、中、右三个部分的内部也做顺序要求，要求每部分里的节点从左到右的顺序与原链表中节点的先后次序一致。
例如：链表9->0->4->5->1，pivot=3。调整后的链表是0->1->9->4->5。在满足原问题要求的同时，左部分节点从左到右为0、1。在原链表中也是先出现0，后出现1；中间部分在本例中为空，不再讨论；右部分节点从左到右为9、4、5。在原链表中也是先出现9，然后出现4，最后出现5。
如果链表长度为N，时间复杂度达到O(N)，额外空间复杂度请达到O(1)。

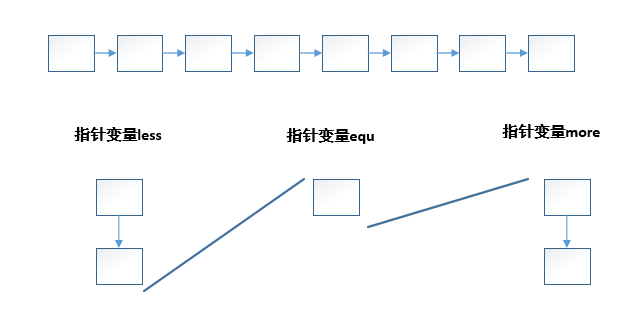
算法思想

遍历链表，设置三个指针变量，小于pivot的节点挂在less指针变量下；
大于pivot的节点挂在more指针下；
等于pivot的节点挂在equ指针变量下。
最后再依次遍历三个指针变量即可。

Retrieve

判定回文结构

需求描述

给定一个链表的头节点head，请判断该链表是否为回文结构。
例如： 1->2->1，返回true。 1->2->2->1，返回true。15->6->15，返回true。 1->2->3，返回false。
如果链表长度为N，时间复杂度达到O(N)，额外空间复杂度达到O(1)。

注意：凡是链表类的题，笔试时用最容易想到的，时间复杂度O(N)，空间复杂度O(N)的；面试时用时间复杂度O(N)，空间复杂度O(1)的；

算法1：时间复杂度O(N)，空间复杂度O(N)。笔试使用！

使用栈，遍历一遍链表把每个节点都压入栈中，这样在弹出栈的时候，所有的节点就逆序了。依次对比原链表的每个节点即可。

算法2：时间复杂度O(N)，空间复杂度O(N/2)。笔试使用！

也使用栈，但是这次只将链表的后半部分（使用2倍的快慢指针）压入栈中，这样在弹出栈的时候，后半部分的节点就逆序了。依次对比链表的前半部分和栈中的每个节点即可。

算法3：时间复杂度O(N)，空间复杂度O(1)。面试使用！

首先改变链表右半区的结构，使整个右半区的指针反指，中间节点的next指向NULL。接下来从两端开始向中间依次对比即可。需要注意的是，再判断完毕后要将链表调整回原链表的结构。

双链表

定义：双向链表也叫双链表，它的每个数据结点中都有两个指针（保存两个节点的地址），分别指向直接后继和直接前驱。

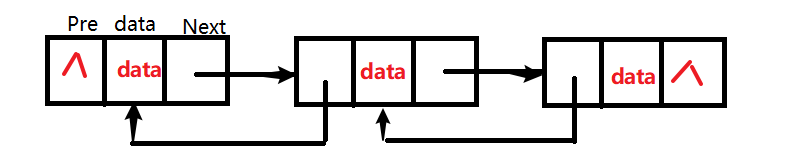
双链表的代码定义：

typedef struct node
{
	int data;
	struct node* pre; //前驱
	struct node* next; //后继
}Node;

特性：

从双向链表中的任意一个结点开始，都可以很方便地访问它的前驱结点和后继结点。
循环链表的最后一个结点指向头结点，循环链表的操作和单链表的操作基本一致，差别仅仅在于算法中的循环条件有所不同。
双向链表使单链表中扩展出来的结构，因此有一部分操作与单链表是相同的，如求长度函数、查找元素位置、打印函数、销毁函数等，这些函数操作都只要涉及一个方向的指针即可。

第一个双链表

#include <stdio.h>
#include <malloc.h>
#include <assert.h>

typedef struct node
{
	int data;
	struct node* pre;
	struct node* next;
}Node; //struct node 完全等于 Node（结构体变量）
typedef Node* LinkList; //struct node * 完全等于 LinkList（结构体指针）

int main()
{
	LinkList head = (LinkList)malloc(sizeof(Node));
	assert(head != NULL);  //检查malloc之后是不是空间不够，返回了空指针NULL（WarningC6011：取消对NULL指针的引用）
	LinkList NodeAa = (LinkList)malloc(sizeof(Node));
	assert(NodeAa != NULL);
	LinkList NodeBb = (LinkList)malloc(sizeof(Node));
	assert(NodeBb != NULL);
	LinkList NodeCc = (LinkList)malloc(sizeof(Node));
	assert(NodeCc != NULL);

	head->data = 101;
	head->pre = NULL;
	head->next = NodeAa;

	NodeAa->data = 202;
	NodeAa->pre = head;
	NodeAa->next = NodeBb;

	NodeBb->data = 303;
	NodeBb->pre = NodeAa;
	NodeBb->next = NodeCc;

	NodeCc->data = 404;
	NodeCc->pre = NodeBb;
	NodeCc->next = NULL;  //单链表中：NodeCc->next = NULL;

	LinkList p = head; //把链表头结点的下一个交给指针p，去遍历
	printf("顺序遍历：");
	while (p != NULL)
	{
		printf("%d  ", p->data);
		p = p->next;
	}

	printf("\n逆序遍历：");
	LinkList tail = NodeCc;
	p = tail;
	while (p != NULL)
	{
		printf("%d  ", p->data);
		p = p->pre;
	}

	return 0;
}

循环单链表

将单链表中终端结点的指针端由 NULL 改为 指向头结点 ，就使整个单链表形成一个环，这种头尾相接的单链表称为单循环链表，简称循环链表。

两种情形：为使空链表与非空链表处理一致，通常设置一个头结点。但并非必须设置头结点。

循环单链表特征：

对于单链表而言，最后一个结点指向NULL；把最后一个结点的不指向NULL而指向头，就是循环单链表；
在单循环链表上的操作基本上与非循环链表相同。循环链表和单链表的主要差异就在于循环的条件判断上，原来是 p->next == NULL，现在是 p->next != 头结点，则循环未结束。
单循环链表可以从表中任意结点开始遍历整个链表，不仅如此，有时对链表常做的操作是在表尾、表头进行。如果用头指针表示循环链表，则需O(n) 时间找到最后一个结点。若改用尾指针表示循环链表，此时查找开始结点和终端结点都很方便了。查找终端结点时间是O(1)，而开始结点，其实就是 rear->next->next ，其时间复杂也为O(1)。

第一个循环单链表

#include <stdio.h>
#include <malloc.h>
#include <assert.h>

typedef struct node
{
	int data;
	struct node* next;
}Node; //struct node 完全等于 Node（结构体变量）
typedef Node* LinkList; //struct node * 完全等于 LinkList（结构体指针）

int main()
{
	LinkList head = (LinkList)malloc(sizeof(Node));
	assert(head != NULL);  //检查malloc之后是不是空间不够，返回了空指针NULL（WarningC6011：取消对NULL指针的引用）
	LinkList NodeAa = (LinkList)malloc(sizeof(Node));
	assert(NodeAa != NULL);
	LinkList NodeBb = (LinkList)malloc(sizeof(Node));
	assert(NodeBb != NULL);
	LinkList NodeCc = (LinkList)malloc(sizeof(Node));
	assert(NodeCc != NULL);

	head->data = NULL; //头结点，不保存数据
	head->next = NodeAa;
	NodeAa->data = 202;
	NodeAa->next = NodeBb;
	NodeBb->data = 303;
	NodeBb->next = NodeCc;
	NodeCc->data = 404;
	NodeCc->next = head;  //单链表中：NodeCc->next = NULL;

	LinkList p = head->next; //把链表头结点的下一个节点，交给指针p，去遍历
	while (p != head)
	{
		printf("%d  ", p->data);
		p = p->next;
	}

	return 0;
}

Create

合并两个循单

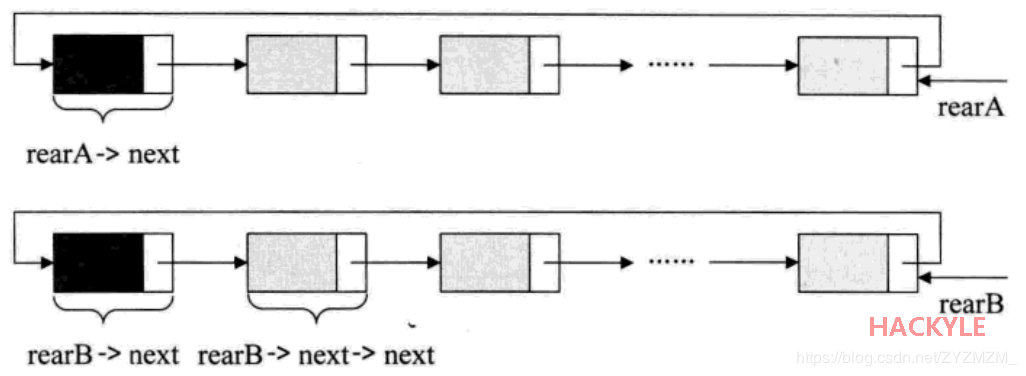
合并操作：A链的尾部指向B链的头部，B链的尾部指向A链的头部

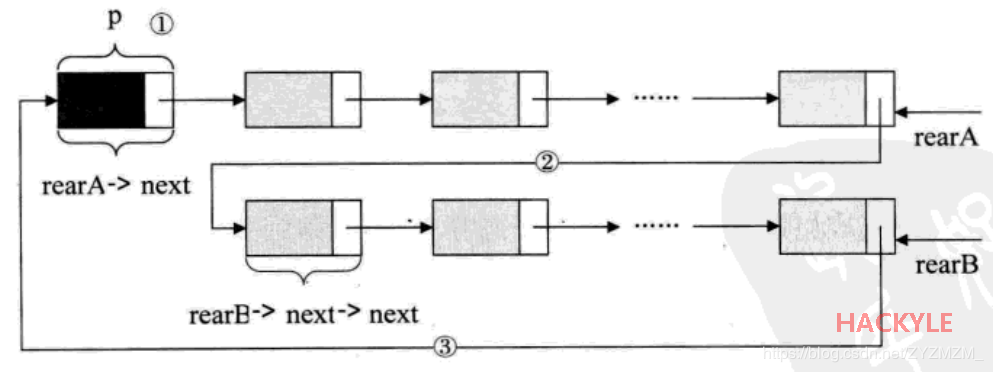
循环双链表

双向链表也叫双链表，它的每个数据结点中都有两个指针（保存两个节点的地址），分别指向直接后继和直接前驱。

头指针的前驱指向最后一个节点，最后一个节点的后继指向头指针。

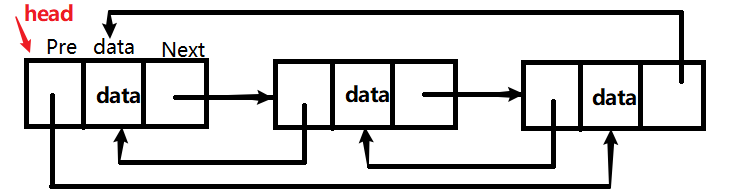
双链表的代码定义：

typedef struct node
{
	int data;
	struct node* pre; //前驱
	struct node* next; //后继
}Node;

特性：

从双向链表中的任意一个结点开始，都可以很方便地访问它的前驱结点和后继结点。
循环链表的最后一个结点指向头结点，循环链表的操作和单链表的操作基本一致，差别仅仅在于算法中的循环条件有所不同。
双向链表使单链表中扩展出来的结构，因此有一部分操作与单链表是相同的，如求长度函数、查找元素位置、打印函数、销毁函数等，这些函数操作都只要涉及一个方向的指针即可。

两种情形：

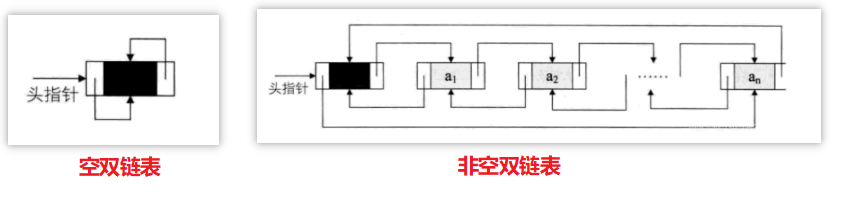
第一个循环双链表

#include <stdio.h>
#include <malloc.h>
#include <assert.h>

typedef struct node
{
	int data;
	struct node* pre;
	struct node* next;
}Node; //struct node 完全等于 Node（结构体变量）
typedef Node* LinkList; //struct node * 完全等于 LinkList（结构体指针）

int main()
{
	LinkList head = (LinkList)malloc(sizeof(Node));
	assert(head != NULL);  //检查malloc之后是不是空间不够，返回了空指针NULL（WarningC6011：取消对NULL指针的引用）
	LinkList NodeAa = (LinkList)malloc(sizeof(Node));
	assert(NodeAa != NULL);
	LinkList NodeBb = (LinkList)malloc(sizeof(Node));
	assert(NodeBb != NULL);
	LinkList NodeCc = (LinkList)malloc(sizeof(Node));
	assert(NodeCc != NULL);

	head->data = NULL; //头结点，不保存数据
	head->pre = NodeCc;
	head->next = NodeAa;

	NodeAa->data = 202;
	NodeAa->pre = head;
	NodeAa->next = NodeBb;

	NodeBb->data = 303;
	NodeBb->pre = NodeAa;
	NodeBb->next = NodeCc;

	NodeCc->data = 404;
	NodeCc->pre = NodeBb;
	NodeCc->next = head;  //单链表中：NodeCc->next = NULL;

	LinkList p = head->next; //把链表头结点的下一个交给指针p，去遍历
	printf("顺序遍历：");
	while (p != head)
	{
		printf("%d  ", p->data);
		p = p->next;
	}

	printf("\n逆序遍历：");
	p = p->pre;
	while (p != head)
	{
		printf("%d  ", p->data);
		p = p->pre;
	}

	return 0;
}

posted @ 2023-01-04 10:32 HACKYLE 阅读(204) 评论(0) 编辑收藏举报

刷新页面返回顶部

hackyle

顺序表的基本操作与重要思想

线性顺序表(数组)

基本操作

Create

Delete

Update

基本思想

链式顺序表

单链

Create

Delete

Update

Retrieve

双链表

第一个双链表

循环单链表

第一个循环单链表

Create

循环双链表

第一个循环双链表

公告