363. Max Sum of Rectangle No Larger Than K

问题：

给定二维数组，

求其中子矩形中元素和不大于K 的最大和。

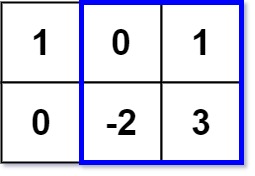
Example 1:
Input: matrix = [[1,0,1],[0,-2,3]], k = 2
Output: 2
Explanation: Because the sum of the blue rectangle [[0, 1], [-2, 3]] is 2, and 2 is the max number no larger than k (k = 2).

Example 2:
Input: matrix = [[2,2,-1]], k = 3
Output: 3
 

Constraints:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-100 <= matrix[i][j] <= 100
-10^5 <= k <= 10^5

　　

example 1:

 

 

解法：preSum（前缀和）

以往我们使用preSum方法，都是在一维数组中。

而这次需要在二维数组中使用，则需要进行降维。

 

 

 

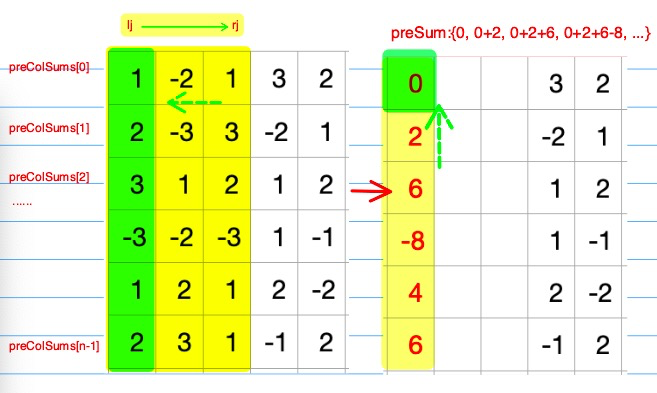
 固定列的范围：lj～rj （外层再进行遍历所有范围可能）

对于任意行 i：将多列压缩成一列->preColSum[i]

这样，我们得到多行的列压缩结果。

这样，就成了一维。{0,2,6,-8,4,6}

对这个一维数组，进行前缀和求解即可。

 

求任意区间的和<=K, 中求最大和。

这里，我们使用二分查找，进行快速查找。

利用辅助前缀和set：preSum

来保存已经遍历过的前缀和。

那么要求的，即为前缀和preSum中 >=当前前缀和curSum-K

这里，由于set是排序set，使用lower_bound即可找到第一个>=curSum-K的数x

即 K>=curSum-x

再将当前前缀和curSum加入已遍历前缀和set：preSum。

 

代码参考：

class Solution {
public:
    int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
        int res=INT_MIN;
        int n = matrix.size(), m = matrix[0].size();
        for(int lj=0; lj<m; lj++) {
            vector<int> preColSums(n,0);//->==rows |<-
            //combine left:<- col[lj ~ rj]
            for(int rj=lj; rj<m; rj++) {
                //in one row, width=[lj, rj]
                for(int i=0; i<n; i++) {
                    preColSums[i] += matrix[i][rj];
                }
                set<int> preSum={0};//preSum need a 0 as minus data
                int curSum=0;
                //combine up ↑
                for(int i=0; i<n; i++) {
                    curSum+=preColSums[i];
                    auto it = preSum.lower_bound(curSum-k);
                    if(it!=preSum.end()) res=max(res, curSum-*it);
                    preSum.insert(curSum);
                }
            }
        }
        return res;
    }
};