496. Next Greater Element I

问题：

给定数组num2，

求num1中各数右边第一个大于它的数。

Example 1:
Input: nums1 = [4,1,2], nums2 = [1,3,4,2]
Output: [-1,3,-1]
Explanation:
For number 4 in the first array, you cannot find the next greater number for it in the second array, so output -1.
For number 1 in the first array, the next greater number for it in the second array is 3.
For number 2 in the first array, there is no next greater number for it in the second array, so output -1.

Example 2:
Input: nums1 = [2,4], nums2 = [1,2,3,4]
Output: [3,-1]
Explanation:
For number 2 in the first array, the next greater number for it in the second array is 3.
For number 4 in the first array, there is no next greater number for it in the second array, so output -1.
 

Constraints:
1 <= nums1.length <= nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 10^4
All integers in nums1 and nums2 are unique.
All the integers of nums1 also appear in nums2.

　　

解法：Monotonic stack（单调栈）

参考：单调栈&单调队列详解

 

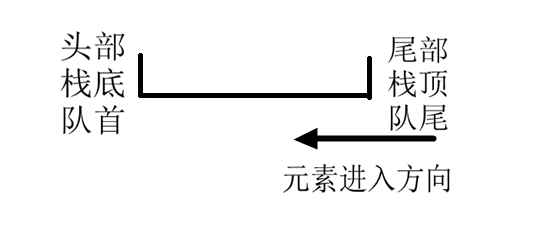
对单调栈or队列的pop操作都在：尾部（stack.top & queue.back<因此得用deque，而不用queue>）

❤️  ！！POINT：

• 动作：要插入新元素
• 要求：要保持栈or队列的状态为递增（递减）
  • 不满足要求：则pop已有元素，再插入当前元素。

特点：

• <常用🌟 >单调递增 栈 （递减队列->可求区间最大值front）(front)<-[4,3,2,1<-top(back)
  • 保存离现在cur最近index为止，最大值的递增序列
• 单调递减 栈 （递增队列->可求区间最小值front）(front)<-[1,2,3,4<-top(back)
  • 保存离现在cur最近index为止，最小值的递减序列

 

增减性 定义：

• stack
  • 单调增 栈：top->bottom 递增↗️     [4,3,2,1<-top
    • while( !stack.empty() && stack.top<=cur ) pop
    • stack.push(cur)
  • 单调减 栈：top->bottom 递减↘️     [1,2,3,4<-top
    • while( !stack.empty() && stack.top>=cur ) pop
    • stack.push(cur)

　解说：

具体进栈过程
对于单调递增栈，若当前进栈元素为e，从栈顶开始遍历元素，把小于e或者等于e的元素弹出栈，直接遇到一个大于e的元素或者栈为空为止，然后再把e压入栈中。
对于单调递减栈，则每次弹出的是大于e或者等于e的元素。

　　

• deque（固定capacity）
  • 单调增 队列：front->back 递增↗️     <-[1,2,3,4]<-back
    • while( !deque.empty() && deque.back>=cur ) pop_back
    • deque.push_back(cur)
  • 单调减 队列：front->back 递减↘️     <-[4,3,2,1]<-back
    • while( !deque.empty() && deque.back<=cur ) pop_back
    • deque.push_back(cur)

 解说：

具体入队过程
对于单调递增队列，设当前准备入队的元素为e，从队尾开始把队列中的元素逐个与e对比，把比e大或者与e相等的元素逐个删除，直到遇到一个比e小的元素或者队列为空为止，然后把当前元素e插入到队尾。
对于单调递减队列也是同样道理，只不过从队尾删除的是比e小或者与e相等的元素。

　　

可求解问题：（例如：单调增栈 [4,3,2,1<-3）需要pop 1, 2, 3

两个方向：

• 当前元素 (cur=3)
  • 左边区间，第一个>cur的数 4。
• 被弹出的元素 stack.top (1,2,3)
  • 右边第一个>=自己的数 cur=3。

单调队列：

• 单调减 front->back 递减↘️     <-[4,3,2,1]<-back
  • 区间最大值：front
• 单点增 front->back 递增↗️     <-[1,2,3,4]<-back
  • 区间最小值：front

参考例题：239. Sliding Window Maximum 

 

本题解法：

要求每个元素右边第一个>自己的数。

有上面的思路，我们可以站在被弹出元素的角度，

使用单调递增栈，来解决。

 

另，求num1中对应num2中的各个元素num。

可引入unordered_map来解决对应关系。

• key：num
• value：所求下一个更大元素。

 

代码参考：

class Solution {
public:
    vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
        unordered_map<int, int> mp;//num_value:res
        vector<int> res;
        stack<int> s;
        for(int n:nums2) {
            while(!s.empty() && s.top()<n) {
                mp[s.top()]=n;
                s.pop();
            }
            s.push(n);
        }
        for(int n1:nums1) {
            res.push_back(mp.count(n1)?mp[n1]:-1);
        }
        return res;
    }
};