372. Super Pow

问题：

求a^b%base的值。

a为int型数

b为int数组，例如[1,2,3,4]代表：b=1234

base=1337。

Example 1:
Input: a = 2, b = [3]
Output: 8

Example 2:
Input: a = 2, b = [1,0]
Output: 1024

Example 3:
Input: a = 1, b = [4,3,3,8,5,2]
Output: 1

Example 4:
Input: a = 2147483647, b = [2,0,0]
Output: 1198

Constraints:
1 <= a <= 2^31 - 1
1 <= b.length <= 2000
0 <= b[i] <= 9
b doesn't contain leading zeros.

　　

解法：math，DFS，Backtracking

参考：labubadong

首先，基本DFS规律为：

 

• part1=a^4
• part2=(a^[1,5,6]) ^10

构建自己的pow方法：mypow

能够计算 a^b

• part1=mypow(a,4)
• part2=mypow(backtrack(a,[1,5,6]),10)

最后结果res=( part1*part2 )%base

 

构建mypow方法：

为了快速计算，我们分奇偶数进行：

 

 

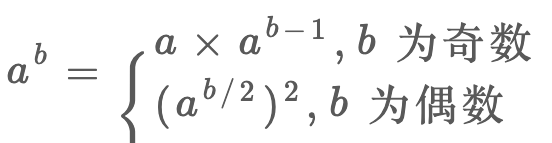
 mypow(a,b)=

• a*mypow(a,b-1), b%2!=0
• mypow(a,b/2)*mypow(a,b/2), b%2==0

 

代码参考：

class Solution {
public:
    int base = 1337;
    //c=a*b
    //c%k=(a%k)*(b%k)%k
    int myPow(int a, int b) {
        if(b==0) return 1;
        a = a%base;
        if(b%2) {//odd
            return (a * myPow(a,b-1)) % base; 
        } else {//even
            int part = myPow(a,b/2);
            return (part*part) % base;
        }
    }
    int superPow(int a, vector<int>& b) {
        if(b.empty()) return 1;
        int cur = b.back();
        int part1 = myPow(a, cur);
        int part2 = 1;
        b.pop_back();
        if(!b.empty()) part2=myPow(superPow(a,b), 10);
        return (part1*part2)%base;
    }
};