221. Maximal Square

问题：

给定有0和1构成的二维数组，

求数组中，连续 1 构成正方形的面积最大是多少。

Example 1:
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 4

Example 2:
Input: matrix = [["0","1"],["1","0"]]
Output: 1

Example 3:
Input: matrix = [["0"]]
Output: 0

Constraints:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] is '0' or '1'.

　　

example 1:

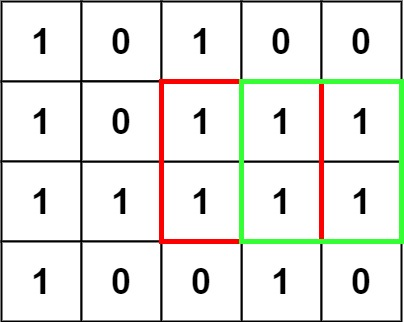
example 2:

 

 

解法：DP

1.状态：dp[i][j]

• i，j：matrix[0~i][0~j]：包含最后一个cell在内，构成的最大满足题意的正方形 边长。

2.选择：

• matrix[i][j]==0：dp[i][j]=0
• matrix[i][j]==1：dp[i][j]= min {↖️左上格子为止最大正方形边长， ↑上方格子为止最大正方形边长，←右方格子为止最大正方形边长} + 1（扩展一格）
•                                = min { dp[i-1][j-1],                               dp[i-1][j],                               dp[i][j-1]                             } + 1

3.base：

• matrix[0][j]=0
• matrix[i][0]=0

4.♻️ 优化：dp由2维降维->1维

j不变，去掉 i。

• tmp保存本次即将被覆盖的dp[j]
  • pre保存dp[j-1]（原来👈 左边格子）最后将tmp赋给它。
• dp[j]代表原来⬆️ 上边格子。
• dp[j-1]代表原来↖️左上格子。

 

代码参考：

class Solution {
public:
    //dp[i][j]: matrix[0~i][0~j] (last cell is 1) : max square's side length.
    //opt:
    //case_1: matrix[i][j]==0 -> dp[i+1][j+1]=0
    //case_2: matrix[i][j]==1 -> dp[i+1][j+1]= min{dp[i-1][j], dp[i][j-1], dp[i-1][j-1]} + 1
    //base:
    //dp[0][0]=0
    //dp[0][j]=0
    //dp[i][0]=0
    int maximalSquare(vector<vector<char>>& matrix) {
        int n=matrix.size(), m=matrix[0].size();
        vector<int>dp(m+1, 0);
        int maxlen = 0;
        int pre=0;
        for(int i=1; i<=n; i++) {
            for(int j=1; j<=m; j++) {
                int tmp = dp[j];
                if(matrix[i-1][j-1]=='0') dp[j]=0;
                else {
                    dp[j] = min(min(pre, dp[j]), dp[j-1]) +1;
                }
                maxlen = max(maxlen, dp[j]);
                pre = tmp;
            }
        }
        return maxlen*maxlen;
    }
};