1519. Number of Nodes in the Sub-Tree With the Same Label

问题：

给定一棵以0为root的树，

给定

• 该树的节点连接关系。
• 每个节点上标记的字母。

求以各个节点为root的子树中，拥有和该节点标记字母相同节点的个数。

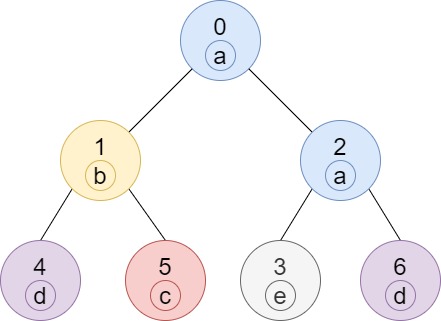
Example 1:
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
Output: [2,1,1,1,1,1,1]
Explanation: Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).

Example 2:
Input: n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
Output: [4,2,1,1]
Explanation: The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.

Example 3:
Input: n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
Output: [3,2,1,1,1]

Example 4:
Input: n = 6, edges = [[0,1],[0,2],[1,3],[3,4],[4,5]], labels = "cbabaa"
Output: [1,2,1,1,2,1]

Example 5:
Input: n = 7, edges = [[0,1],[1,2],[2,3],[3,4],[4,5],[5,6]], labels = "aaabaaa"
Output: [6,5,4,1,3,2,1]
 

Constraints:
1 <= n <= 10^5
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
labels.length == n
labels is consisting of only of lower-case English letters.

example 1:

​

example 2:

​

example 3:

​

解法：DFS

• 状态：
  • 当前节点id
  • 当前节点为root的子树中，各个字母的出现次数统计。
• 选择：
  • 当前节点的子节点
    • （使用res[i]标记当前节点是否为父节点。每次处理中，对于当前节点结束后，才更新当前节点的res。
    • 因此，若当前节点的res已经!=0初始值，那么证明该节点为父节点。）
• 处理：
  • 更新当前节点的res为1。（自己字母累计）
  • 对所有子节点统计，各个子树cnt1的所有字母总和。
  • 对当前节点的字母总和cnt即为：同一个字母的各个子树上的计数和。
  • 当前节点的res则为：res = cnt[当前节点字母]+1（自己）

 

代码参考：

class Solution {
public:
    unordered_map<int, vector<int>> graph;
    int N;
    void dfs(vector<int>& res, int cnt[], int root, string& labels) {
        if(res[root]!=0) return;//except for parent who will already count res
        res[root] = 1;
        for(auto child:graph[root]) {
            int cnt1[26] = {0};
            //cnt: In current root node's subtree, the count of each alphbet.
            //cnt1: In child node's subtree, the count of each alphbet.
            dfs(res, cnt1, child, labels);
            for(int k=0; k<26; k++)
                cnt[k]+=cnt1[k];
        }
        cnt[labels[root]-'a']+=1;
        res[root] = cnt[labels[root]-'a'];
        return;
    }
    vector<int> countSubTrees(int n, vector<vector<int>>& edges, string labels) {
        vector<int> res(n,0);
        int cnt[26] = {0};
        N = n;
        for(auto ed:edges) {
            graph[ed[0]].push_back(ed[1]);
            graph[ed[1]].push_back(ed[0]);
        }
        dfs(res, cnt, 0, labels);
        return res;
    }
};