1284. Minimum Number of Flips to Convert Binary Matrix to Zero Matrix

问题：

给定m*n由0和1构成的二维数组，

对其中某个元素进行反转flip：0->1 or 1->0

那么其相邻的元素也会相应发生反转。

求，最终使得二维数组全为0需要最少几步？

若不能做到，返回-1。

Example 1:
Input: mat = [[0,0],[0,1]]
Output: 3
Explanation: One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.

Example 2:
Input: mat = [[0]]
Output: 0
Explanation: Given matrix is a zero matrix. We don't need to change it.

Example 3:
Input: mat = [[1,1,1],[1,0,1],[0,0,0]]
Output: 6

Example 4:
Input: mat = [[1,0,0],[1,0,0]]
Output: -1
Explanation: Given matrix can't be a zero matrix
 
Constraints:
m == mat.length
n == mat[0].length
1 <= m <= 3
1 <= n <= 3
mat[i][j] is 0 or 1.

　　

example 1:

 

 

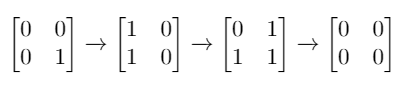
解法：BFS + bitset

• 状态：当前的数组状况，使用bitset进行记录。
  • visited：记录bitset->string：省略比较方法==
• 选择：
  • 对所有cell，尝试反转。若已存在于visited的状态，不再加入queue。

 

bitset：

• 构造体：bitset<n> :⚠️ 注意：n必须为常数，不能为变量。
  • 默认初始化为全 0。
• 方法：
  • count：统计 1 的个数。
  • flip(index)：对第index位进行反转（index:0~n-1，从右向左 👈 ）
  • set(index)：默认：对第index位置 1。
    • set(index, 0)：对第index位置 0。
  • to_string：转化为字符串。

 

代码参考：

class Solution {
public:
    int m,n;
    int dir[5] = {1,0,-1,0,1};
    bitset<9> getstate(bitset<9>& state, int i, int j) {
        bitset<9> next = state;
        //vector<vector<int>> memo;
        next.flip(i*m+j);
        for(int d=1; d<5; d++) {
            int x = i+dir[d-1];
            int y = j+dir[d];
            if(x<0 || y<0 || x>=n || y>=m) continue;
            next.flip(x*m+y);
            //memo.push_back({x,y});
        }
       // if(next.count()==0) {
       //     cout<<"state:"<<state.to_string()<<endl;
       //     cout<<"i: "<<i<<" ; j: "<<j<<endl;
       //     cout<<"flip:"<<endl;
       //     for(auto m:memo) cout<<"x:"<<m[0]<<", y:"<<m[1]<<endl;
       // }
        return next;
    }
    int minFlips(vector<vector<int>>& mat) {
        n=mat.size();
        m=mat[0].size();
        bitset<9> state;
        int step = 0;
        for(int i=0; i<n; i++) {
            for(int j=0; j<m; j++) {
                if(mat[i][j]) state.set(i*m+j);
            }
        }
        //cout<<"START:"<<state.to_string()<<endl;
        queue<bitset<9>> q;
        unordered_set<string> visited;
        if(state.count()==0) return 0;
        q.push(state);
        visited.insert(state.to_string());
        while(!q.empty()) {
            int sz = q.size();
            for(int k=0; k<sz; k++) {
                auto cur = q.front();
                q.pop();
                //cout<<"pop:"<<cur.to_string()<<endl;
                if(cur.count()==0) return step;
                for(int i=0; i<n; i++) {
                    for(int j=0; j<m; j++) {
                        auto next = getstate(cur, i, j);
                        if(visited.insert(next.to_string()).second) {
                            q.push(next);
                            //cout<<"push:"<<next.to_string()<<endl;
                        }
                    }
                }
            }
            step++;
        }
        return -1;
    }
};