913. Cat and Mouse

问题：

给定一个无向图，节点0～N-1

• mouse：从1出发->  到达 0，win -> return 1
• cat：从2出发-> 到达mouse的当前位置，win（不能走 0 节点）-> return 2
• 若两者都无法win，且走完所有的节点，那么平局 tie。-> return 0

⚠️ 注意：

• mouse和cat都不能重复走同一个节点。
• mouse先出发。

Example 1:
Input: graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]]
Output: 0

Example 2:
Input: graph = [[1,3],[0],[3],[0,2]]
Output: 1

Constraints:
3 <= graph.length <= 50
1 <= graph[i].length < graph.length
0 <= graph[i][j] < graph.length
graph[i][j] != i
graph[i] is unique.
The mouse and the cat can always move. 

　　

example 1:

 

 

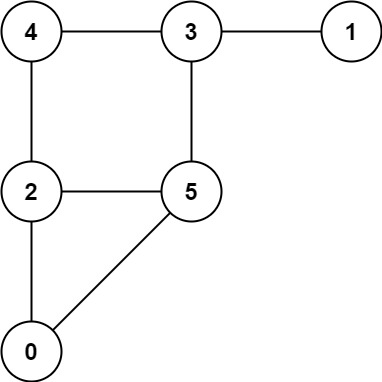
example 2:

 

 

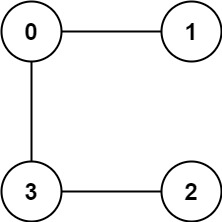
解法：DFS+DP

状态：

• POS_mouse
• POS_cat
• time(steps)

dp[m][c][t]：mouse在m节点，cat在c节点，在t步时（以后各种走法之后），是谁输谁赢

• 0：平局
• 1：mouse赢
• 2：cat赢

选择（状态转移）：dp[m][c][t] = ？

• 当前是mouse走：
  • 若下一步 dp[m_next][c][t+1]
    • 有一种mouse能赢的方法：则 dp[m][c][t] = 1（mouse赢）
    • 所有都不能使得mouse赢，但存在可以平局的方法：则 dp[m][c][t] = 0（平局）
    • 既不能赢，也不能平局，所有可能都是输：则 dp[m][c][t] = 2（mouse输）
• 当前是cat走：
  • 若下一步  dp[m][c_next][t+1]
    • 有一种cat能赢的方法：则 dp[m][c][t] = 2（cat赢）
    • 所有都不能使得cat赢，但存在可以平局的方法：则 dp[m][c][t] = 0（平局）
    • 既不能赢，也不能平局，所有可能都是输：则 dp[m][c][t] = 1（cat输）

base：

• t==2*N，步数超出，则mouse和cat一定重复走以前走过的节点，直接返回平局 0。（无胜负之分）
• m==0，mouse走到节点0，mouse赢，返回 1。
• c==m，cat抓到mouse，cat赢，返回 2。

同时，如果存在已经走过的状态，直接返回保存过的dp[m][c][t]

初始化所有dp=-1，当非初始值，则证明已经处理过该状态，直接返回。

 

代码参考：

class Solution {
public:
    //DP:state: pos_mouse, pos_cat, time(step)
    //   size:  N,         N,       2*N
    //dp[m][c][t]:[ mouse_pos=m, cat_pos=c, step=t ] who wins
    // -> 0:tie, 1:mouse win, 2:cat win
    //opt:
    //case_1: mouse's turn: dp[m][c][t] = dp[m_next][c][t+1]
    //        next_step: any route can make to win, mouse will choose. then mouse will win.
    //                   no route can make to win, mouse will choose the tie route.
    //                   all routes would be lose, mouse definitly lose at end.
    //case_2: cat's turn:   dp[m][c][t] = dp[m][c_next][t+1]
    //base:
    //dp[m][c][2N] = 0:tie
    //dp[0][c][t]  = 1:mouse win
    //dp[m][m][t]  = 2:cat win
    int N;
    vector<vector<vector<int>>> dp;
    int dfs(vector<vector<int>>& graph, int m, int c, int t) {
        if(t==2*N) return 0;//tie
        if(dp[m][c][t]!=-1) return dp[m][c][t];
        if(m==0) return dp[m][c][t]=1;
        if(m==c) return dp[m][c][t]=2;
        int who = t%2;
        if(who==0) {//who==0: mouse's turn (cause: Start from mouse by t=0) 
            bool tie_flg = false;
            for(int m_next:graph[m]) {
                int res = dfs(graph, m_next, c, t+1);
                if(res == 1) {//mouse win (最优先)
                    return dp[m][c][t] = 1;
                } else if(res != 2) {//mouse tie route (次优先)
                    tie_flg = true;
                }
            }
            //after all next opts: there is no win method:
            if(tie_flg) return dp[m][c][t] = 0;//prioritly choose tie route.
            return dp[m][c][t] = 2;//mouse lose
        } else {//cat's turn
            bool tie_flg = false;
            for(int c_next:graph[c]) {
                if(c_next==0) continue;
                //it is not allowed for the Cat to travel to the Hole (node 0.)
                int res = dfs(graph, m, c_next, t+1);
                if(res == 2) {//cat win
                    return dp[m][c][t] = 2;
                } else if(res != 1) {//cat tie route
                    tie_flg = true;
                }
            }
            //after all next opts: there is no win method:
            if(tie_flg) return dp[m][c][t] = 0;//prioritly choose tie route.
            return dp[m][c][t] = 1;//cat lose
        }
    }
    int catMouseGame(vector<vector<int>>& graph) {
        N = graph.size();
        //initialize all cell -> -1
        dp.resize(N, vector<vector<int>>(N, vector<int>(2*N, -1)));
        return dfs(graph, 1, 2, 0);//POS(mouse)=1, POS(cat)=2, step=0;
    }
};