865. Smallest Subtree with all the Deepest Nodes

问题：

给定一棵二叉树，

求距离root最远距离d，所有节点所在的公共父节点。

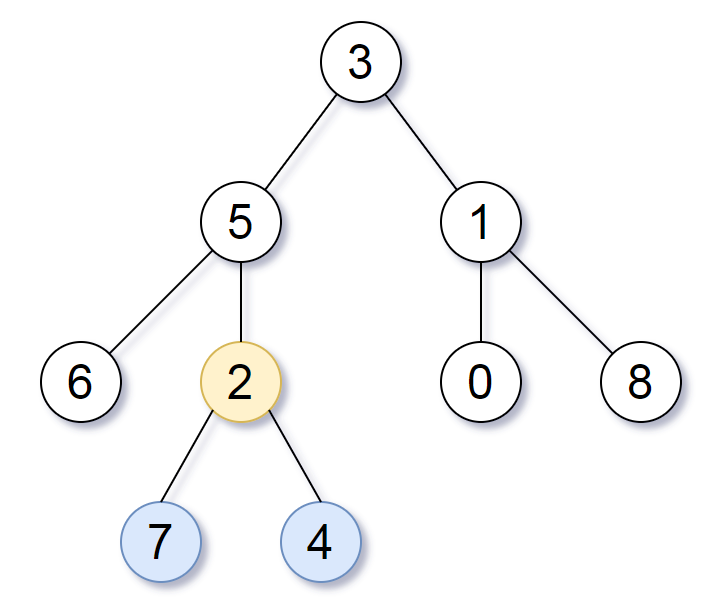
Example 1:
Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
The nodes coloured in blue are the deepest nodes of the tree.
Notice that nodes 5, 3 and 2 contain the deepest nodes in the tree but node 2 is the smallest subtree among them, so we return it.

Example 2:
Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree.

Example 3:
Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest node in the tree is 2, the valid subtrees are the subtrees of nodes 2, 1 and 0 but the subtree of node 2 is the smallest.

Constraints:
The number of nodes in the tree will be in the range [1, 500].
0 <= Node.val <= 500
The values of the nodes in the tree are unique.

　　

example 1:

 

 

解法：DFS

• 状态：当前root节点。
• 需要返回：
  • 当前节点的深度deep
  • 当前节点为止，最深节点的最小公共父节点
• base：
  • root==null，返回 { 深度=0，root自己 }
• 对于当前节点：
  • 递归求子树：
    • 左孩子：!=null, 求出 { 左子树的深度， 左子树中最深节点的最小公共父节点 }
    • 右孩子：!=null, 求出 { 右子树的深度， 右子树中最深节点的最小公共父节点 }
  • 当前节点的结果：
    • 当前节点的深度=max(deep(左子树), deep(右子树))
    • 当前节点的最深节点的最小公共父节点=
      • 如果左右子树一样深，返回root自己。
      • 左子树深，返回左子树的结果（左子树中最深节点的最小公共父节点）。
      • 右子树深，返回右子树的结果（右子树中最深节点的最小公共父节点）。

 

代码参考：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //deep, node
    pair<int,TreeNode*> dfs(TreeNode* root) {
        if(!root) return {0,root};
        pair<int,TreeNode*> left, right;
        if(root->left) left = dfs(root->left);
        if(root->right) right = dfs(root->right);
        if(left.first == right.first) return {left.first+1,root};
        else if(left.first > right.first) {
            return {left.first+1, left.second};
        } else {
            return {right.first+1, right.second};
        }
    }
    TreeNode* subtreeWithAllDeepest(TreeNode* root) {
        return dfs(root).second;
    }
};