【BFS】752. Open the Lock

参考：https://labuladong.gitbook.io/algo/di-ling-zhang-bi-du-xi-lie/bfs-kuang-jia

问题：

求从【0000】四位密码锁初始状态，最少经过几步，能找到给定目标秘密target

另，其中若转到给定deadends的密码，则永远打不开锁，因此需要避开这些密码。

Example 1:
Input: deadends = ["0201","0101","0102","1212","2002"], target = "0202"
Output: 6
Explanation:
A sequence of valid moves would be "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202".
Note that a sequence like "0000" -> "0001" -> "0002" -> "0102" -> "0202" would be invalid,
because the wheels of the lock become stuck after the display becomes the dead end "0102".

Example 2:
Input: deadends = ["8888"], target = "0009"
Output: 1
Explanation:
We can turn the last wheel in reverse to move from "0000" -> "0009".

Example 3:
Input: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"
Output: -1
Explanation:
We can't reach the target without getting stuck.

Example 4:
Input: deadends = ["0000"], target = "8888"
Output: -1
 
Constraints:
1 <= deadends.length <= 500
deadends[i].length == 4
target.length == 4
target will not be in the list deadends.
target and deadends[i] consist of digits only.

　　

解法：BFS（广度优先搜索）

• queue：q：存储每层尝试的节点
• set：visited：存储已经访问过的节点，避免重复访问，形成死循环

框架过程：

• INIT：将start节点加入q和visited中，开始处理尝试q中的所有节点
• （q不为空的情况下，还有层次未尝试）对于每一层尝试
  • INIT：获取当前层q.size，用来界定层次+1
  • 对每一层的所有节点：
    • 判断是否为target？是->return step，否->继续
    • 将当前节点cur的所有邻接节点都加入q和visited中。
      • 条件：这些邻接节点不在visited中（即未曾访问过）
  • 每层所有节点判定完毕，step++。
• 最后都没有找到target的话，即无法找到。

对本问题：

q：储存所有下一步的密码可能。（向上拨一位，向下拨一位，各4位，则共有8中可能）

visited：已经判断过的密码。

⭐️ 特：deadends，若当前判断的密码是deadends中的密码，则放弃尝试，continue到下一个密码的尝试。

 

代码参考：

class Solution {
public:
    //getAdjacentNode
    void pushAdjacentNode(queue<string>& q, unordered_set<string>& visited, string s) {
        for(int i=0; i<4; i++) {
            string up = plusOne(s, i);
            if(visited.count(up)==0) {
                q.push(up);
                visited.insert(up);
            }
            string down = minusOne(s, i);
            if(visited.count(down)==0) {
                q.push(down);
                visited.insert(down);
            }
        }
    }
    string plusOne(string s, int pos) {
        if(s[pos]=='9') s[pos]='0';
        else s[pos]++;
        return s;
    }
    string minusOne(string s, int pos) {
        if(s[pos]=='0') s[pos]='9';
        else s[pos]--;
        return s;
    }
    int openLock(vector<string>& deadends, string target) {
        queue<string> q;
        unordered_set<string> visited;
        unordered_set<string> dead(deadends.begin(), deadends.end());
        int res = 0;
        q.push("0000");
        visited.insert("0000");
        
        while(!q.empty()) {
            int sz = q.size();
            for(int i=0; i<sz; i++) {
                string cur = q.front();
                q.pop();
                if(dead.count(cur) != 0) continue;
                if(cur == target) {
                    return res;
                }
                pushAdjacentNode(q, visited, cur);
            }
            res++;
        }
        return -1;
    }
};

 

解法：Bidirectional BFS（双向 广度优先搜索）

条件：已知target目标节点+初始节点。（只知道初始节点时，只能用单向 BFS）

 

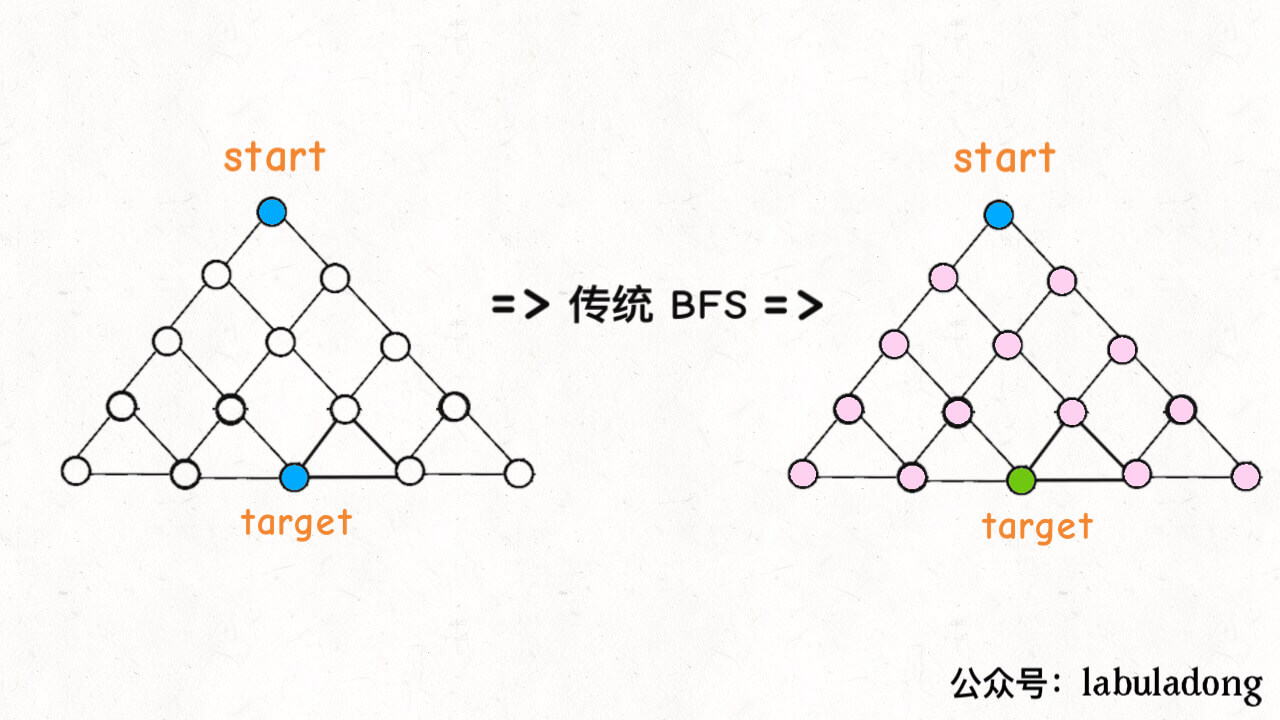
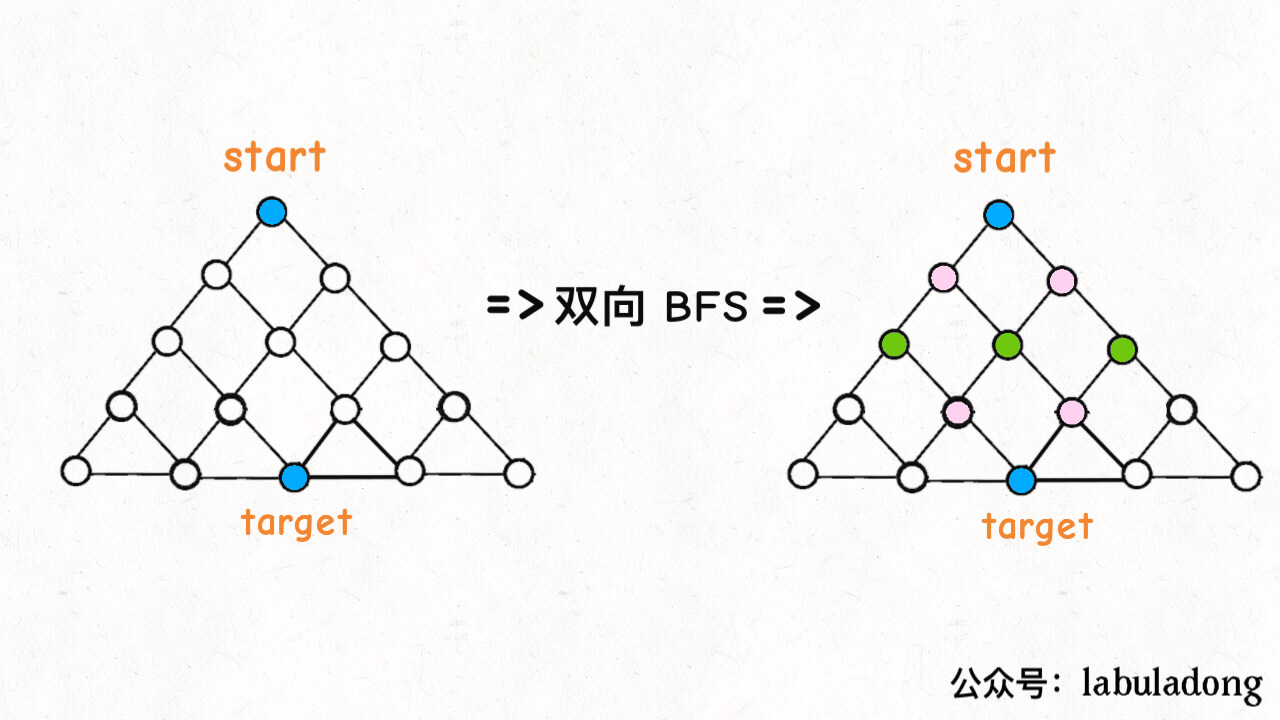
 时间复杂度一样，只是双向BFS从两侧遍历，缩小了半棵树的搜索。

 

 

 实现：

改变内容	单向BFS	双向BFS
遍历对象	queue q（start向下）	unordered_set q1（start向下），q2（target向上）
⚠️ visited添加时机	⭕️ 加入q的同时	⭕️ 马上使用visited之前（由于每次加入visit的节点，实际是为下下一次check对象准备的<不能妨碍下一次check>）
每层遍历新增邻接节点	插入q中	插入每层遍历新作临时set tmp中
判断是否找到	cur==target?	q2.count(cur)!=0?  反向搜索set中是否存在正向搜索的当前节点？
每层判断结束	层数+1，step++	除层数+1外，设置下次循环搜索对象为p2(当前的反向)，tmp为下次循环搜索的p2，丢弃当前搜索完的p1

♻️  优化：使得每次的搜索对象p1的长度最短（遍历次数尽可能少），即当p1.size()>p2.size()则调换swap(p1,p2)。

代码参考：

class Solution {
public:
    //getAdjacentNode
    void pushAdjacentNode(unordered_set<string>& q, unordered_set<string>& visited, string s) {
        for(int i=0; i<4; i++) {
            string up = plusOne(s, i);
            if(visited.count(up)==0) {
                q.insert(up);
                //visited.insert(up);
            }
            string down = minusOne(s, i);
            if(visited.count(down)==0) {
                q.insert(down);
                //visited.insert(down);
                //delay the timing to flag cur visited.
                //cause this visited node is of the next next check obj, not the next check obj.
            }
        }
    }
    string plusOne(string s, int pos) {
        if(s[pos]=='9') s[pos]='0';
        else s[pos]++;
        return s;
    }
    string minusOne(string s, int pos) {
        if(s[pos]=='0') s[pos]='9';
        else s[pos]--;
        return s;
    }
    int openLock(vector<string>& deadends, string target) {
        unordered_set<string> q1;
        unordered_set<string> q2;
        unordered_set<string> visited;
        unordered_set<string> dead(deadends.begin(), deadends.end());
        int res = 0;
        q1.insert("0000");
        q2.insert(target);
        //visited.insert("0000");
        //visited.insert(target);
        
        while(!q1.empty() && !q2.empty()) {
            unordered_set<string> tmp;
            if(q1.size()>q2.size()) {
                swap(q1, q2);
            }
            int sz = q1.size();
            for(string cur : q1) {
                if(dead.count(cur) != 0) continue;
                //if(cur == target) {
                if(q2.count(cur) != 0) {
                    return res;
                }
                visited.insert(cur);//put in visited directly before using visited set.
                pushAdjacentNode(tmp, visited, cur);
            }
            res++;
            //q1 checked over, discard it.
            //and q2 will be the next check object, 
            //tmp is the new object waiting like q2 position.
            q1 = q2;
            q2 = tmp;
        }
        return -1;
    }
};