222. Count Complete Tree Nodes

问题：

计算给定完全二叉树的节点个数。

Example:

Input: 
    1
   / \
  2   3
 / \  /
4  5 6

Output: 6

　

解法：Complete Binary Tree（完全二叉树）　

首先明确以下定义：

 

 

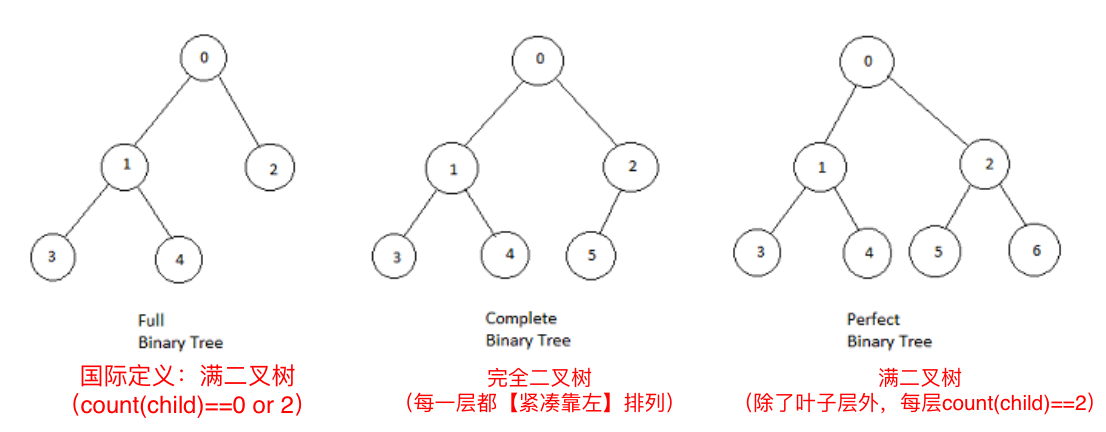
• （了解即可）Full Binary Tree
  • 国际定义的 满二叉树
  • 定义：A binary tree in which each node has exactly zero or two children.In other words, every node is either a leaf or has two children. For efficiency, any Huffman coding is a full binary tree.
  • 

     

     因此这样的二叉树，也叫做 Full Binary Tree

• Complete Binary Tree
  • 完全二叉树
  • 定义：A binary tree in which every level, except possibly the deepest, is completely filled. At depth n, the height of the tree, all nodes must be as far left as possible. 
• Perfect Binary Tree
  • 满二叉树
  • 定义：A binary tree with all leaf nodes at the same depth. All internal nodes have degree 2. 

本题中，

• 函数定义  int countNodes(TreeNode* root)
  • 对每一个root节点，求出本身+递归(所有子节点的个数)和。
  • 一般的，= count(1+countNodes(children))
  • ♻️ 优化：若该完全二叉树，特别的，是满二叉树（Perfect Binary Tree）：
    • 可求出树高height，总节点个数=2^(height)-1
• 状态  root
• 选择  （分别得到左右节点的结果left，right后）
  • return 1+left+right
• base case
  • if(!root) return 0;

时间复杂度：

一般递归次数：树的高度 O(logN)

每次递归时间：（♻️ 优化 求树高花时间=树高）O(logN)

因此，总共花时间：O(logN*logN)

 

代码参考：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //recursion
    //Def: return the count of node
    //     -> full binary tree -> 2^hight-1
    //     -> complete binary tree -> tofind left, right tree, recursionly.
    //Status: root
    //Opt: (after get left,right result)
    //    return left+right+1.
    //base:
    //     root==null: return 0.
    int countNodes(TreeNode* root) {
        if(!root) return 0;
        int lh = 1, rh = 1;
        TreeNode* l = root->left;
        while(l) {
            lh++;
            l = l->left;
        }
        TreeNode* r = root->right;
        while(r) {
            rh++;
            r = r->right;
        }
        //full binary tree
        if(lh==rh) {
            return pow(2,lh)-1;//2^hight-1
        }
        //complete binary tree -> recursion
        lh = countNodes(root->left);
        rh = countNodes(root->right);
        return lh+rh+1;
    }
};