198. House Robber; 213. House Robber II; 337. House Robber III
问题:
base题目:
给定一组数列,代表一排住宅,各自能偷出的钱数。
不能偷取相邻的两家。求能偷出的最大钱数。
- I base题目
-
Example 1: Input: nums = [1,2,3,1] Output: 4 Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3). Total amount you can rob = 1 + 3 = 4. Example 2: Input: nums = [2,7,9,3,1] Output: 12 Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1). Total amount you can rob = 2 + 9 + 1 = 12. Constraints: 0 <= nums.length <= 100 0 <= nums[i] <= 400 - II base题目+首尾两家也互为相邻(住宅为环形,首尾相连)
-
Example 1: Input: [2,3,2] Output: 3 Explanation: You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses. Example 2: Input: [1,2,3,1] Output: 4 Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3). Total amount you can rob = 1 + 3 = 4. - III base题目+住宅为:先序遍历的二叉树(二叉树相连的两个节点互为相邻,不能同时偷取)
-
Example 1: Input: [3,2,3,null,3,null,1] 3 / \ 2 3 \ \ 3 1 Output: 7 Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7. Example 2: Input: [3,4,5,1,3,null,1] 3 / \ 4 5 / \ \ 1 3 1 Output: 9 Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.
解法:
I base题目:DP(动态规划)
1.确定【状态】:
- 到当前为止的住宅:第 i 家
2.确定【选择】:
- 选择 1(偷取 当前的第 i 家):
- dp[i-2] + nums[i] :不能偷取相邻的前一家,只能从上上一家为止中进行选择 + 偷取当前家的钱数。
- 选择 2 (不偷取 当前的第 i 家):
- dp[i-1]:可以偷取相邻的前一家,从到前一家为止中进行选择
3. dp[i]的含义:
到第i家为止,能偷取获得的最大钱数。
4. 状态转移:
dp[i]= MAX {
- 选择 1 (偷取 当前的第 i 家):dp[i-2] + nums[i]
- 选择 2 (不偷取 当前的第 i 家):dp[i-1]
}
5. base case:
- i==0:没有一家的住宅,最多能偷取钱数为0
- dp[0] = 0
- i==1:只有一家的住宅,最多即能偷取这一家,钱数为nums[0]
- dp[1] = nums[0]
代码参考:
1 class Solution { 2 public: 3 //dp[i]: in first i houses, the max money we can get 4 // = max(case_1, case_2) 5 //case_1: choose i-th house 6 // dp[i-2] + nums[i] 7 //case_2: not choose i-th house 8 // dp[i-1] 9 //base case: 10 // dp[0]=0 11 // dp[1]=nums[0] 12 int rob(vector<int>& nums) { 13 int n = nums.size(); 14 if(n<=0) return 0; 15 vector<int> dp(n+1, 0); 16 dp[1] = nums[0]; 17 for(int i=2; i<=n; i++) { 18 dp[i] = max(dp[i-2]+nums[i-1], dp[i-1]); 19 } 20 return dp[n]; 21 } 22 };
♻️ 优化:
空间复杂度:2维->1维
去掉 i
需要前一次的dp[1] ->dp_pre0
还有前前一次的dp[0] ->dp_pre1
代码参考:
1 class Solution { 2 public: 3 int rob(vector<int>& nums) { 4 int n = nums.size(); 5 if(n<=0) return 0; 6 int dp_pre0=nums[0], dp_pre1=0; 7 for(int i=2; i<=n; i++) { 8 int tmp = dp_pre0; 9 dp_pre0 = max(dp_pre1+nums[i-1], dp_pre0); 10 dp_pre1 = tmp; 11 } 12 return dp_pre0; 13 } 14 };
II base题目+首尾两家也互为相邻(住宅为环形,首尾相连)
第一题 DP的基础上,
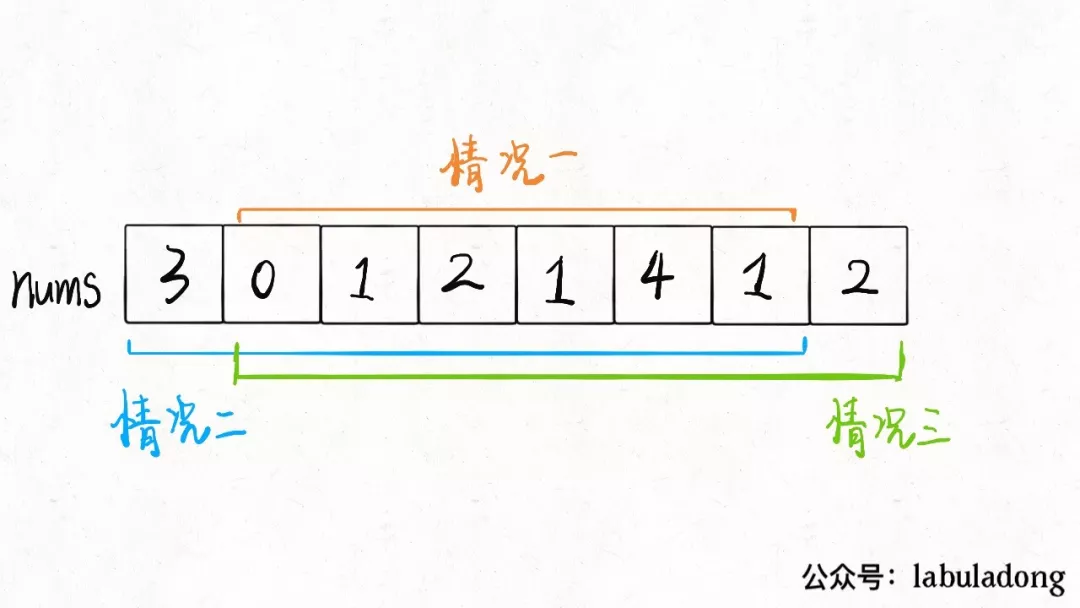
由于 情况一 包含在 情况二 or 情况三 中,因此只需要求得:MAX{ 情况二 , 情况三 }
分别对 情况二 情况三,带入第一题的DP解法中。
求nums[0~n-1] 和 nums[1~n] 的最大值,在取这二者的最大值即可。
代码参考:
1 class Solution { 2 public: 3 int rob(vector<int>& nums) { 4 int n = nums.size(); 5 if(n==1) return nums[0]; 6 return max(robdp(nums, 0, n-1), robdp(nums, 1, n)); 7 } 8 int robdp(vector<int>& nums, int start, int end) {//[start,end) 9 int n = end-start; 10 if(n<=0) return 0; 11 int dp_pre0=nums[start], dp_pre1=0; 12 for(int i=start+2; i<=end; i++) { 13 int tmp = dp_pre0; 14 dp_pre0 = max(dp_pre1+nums[i-1], dp_pre0); 15 dp_pre1 = tmp; 16 } 17 return dp_pre0; 18 } 19 };
III base题目+住宅为:先序遍历的二叉树(二叉树相连的两个节点互为相邻,不能同时偷取)
dp[root][r]:对节点root来说,有两种选择:r=0(选择不偷取)的结果,or r=1(选择偷取)的结果。
要求的最终结果为:max{ dp[root][0], dp[root][1] }
而对root来说:
- 若r=0(选择不偷取):max { dp[left][0], dp[left][1] } + max { dp[right][0], dp[right][1] } 左边右边都可以选择偷取or不偷取,分别取最大,然后相加。
- 若r=1(选择偷取的结果):dp[left][0] + dp[right][0] 左边右边都只能不偷取,相加。
base case: root=null
- dp[root][0] = 0
- dp[root][1] = 0
代码参考:
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode() : val(0), left(nullptr), right(nullptr) {} 8 * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} 9 * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} 10 * }; 11 */ 12 class Solution { 13 public: 14 //dp[root]= 15 //case_1:rob: dp[root][1]= 16 // dp[left][0]+dp[right][0]+root->val 17 //case_2:not_rob: dp[root][0]= 18 // max(dp[left][1],dp[left][0]) 19 // + max(dp[right][1],dp[right][1]) 20 int rob(TreeNode* root) { 21 if(!root) return 0; 22 int* robres=dp(root); 23 return max(robres[0], robres[1]); 24 } 25 int* dp(TreeNode* root) { 26 int *robres = new int[2]{0,0}; 27 if(!root) return robres; 28 int *left = dp(root->left); 29 int *right = dp(root->right); 30 robres[0] = max(left[1], left[0]) + max(right[1], right[0]); 31 robres[1] = left[0] + right[0] + root->val; 32 delete [] left; 33 delete [] right; 34 return robres; 35 } 36 };






