28. Implement strStr() KMP

参考：https://labuladong.gitbook.io/algo/dong-tai-gui-hua-xi-lie/dong-tai-gui-hua-zhi-kmp-zi-fu-pi-pei-suan-fa

问题：实现strstr，求是否为子串，若是，返回子串所在第一个字符的index，否则返回-1。

Example 1:
Input: haystack = "hello", needle = "ll"
Output: 2

Example 2:
Input: haystack = "aaaaa", needle = "bba"
Output: -1

Clarification:
What should we return when needle is an empty string? This is a great question to ask during an interview.
For the purpose of this problem, we will return 0 when needle is an empty string. This is consistent to C's strstr() and Java's indexOf().

Constraints:
haystack and needle consist only of lowercase English characters.

　　

解法：KMP（字符串匹配算法）-> DP（动态规划）

思想：首先有两个字符串：

• 目标字符串 txt
• 模式匹配串（子串）pat

KMP算法的思想：只根据 pat 构建一个状态转移提示字典dp。

根据dp，遍历txt，最后能使状态转移至最终状态，则匹配成功。

 

1.构建dp：参照函数：KMP

这里由于和状态迁移相关，我们很容易想到使用DP来构建辅助字典dp。

• dp[j][c]：在当前状态 j 的情况下，遇到字符c，则需要迁移到的目标状态。
• 状态转移：dp[j][c]=
  • 若c==pat[j]，则向下一个状态迁移：j+1
  • 若c!=pat[j]，则返回 影子状态 X

这里，我们引入 影子状态X 的概念：

• 该状态处于当前状态 j 的一个单位后滞状态。且0～X与0～j字符串拥有（最长）相同前缀。

 

 

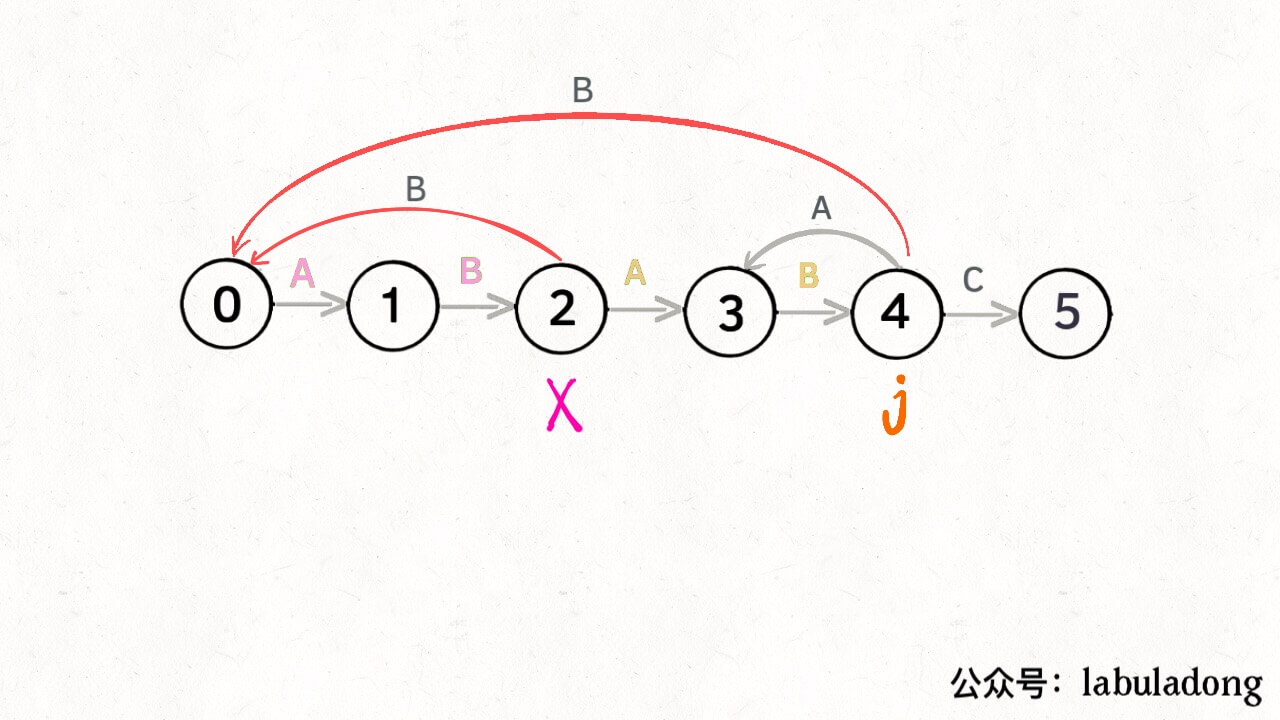
⚠️  如何确定 影子状态X ：

由概念，我们可利用，在前面已经构建好的dp[][]来得知，X=dp[X][pat[j]]

状态为前面的状态X的时候，遇到当前的字符 pat[j] 的迁移方法，

• forward：继续向后迁移状态？相同前缀一起扩展一个字符。
• backward：返回上一个影子状态？相同前缀不再存在。缩小相同前缀的长度。

2.利用dp，匹配目标字符串txt

使用 j 来记录当前状态，初始化为 0。

使用 i 遍历txt，更新每次的状态 j = dp[j][txt[i]]

如果 j = final状态，则返回 i-j+1 为子串开始index

否则继续遍历，直到txt末尾，还未匹配则返回-1。

 

代码参考：

class Solution {
    //dp[j][c]:if we meet the char c when it is in status j, we should move to which status?
    //  case_1: c == pat[j]: dp[j][c] = j+1;
    //  other: dp[j][c] = dp[X][c] (X:the shadow status of j)
    //base case: dp[0][pat[0]] = 1 otherwise dp[0][other] = 0
    //how to fix X:
    //X is just one latter status after j,
    //and X has the same prefix string with j.
    //so we can exploit initialized dp[][] to update X.
    //X = dp[X][pat[j]]
    //has the same move(forward or backward) with preceding status j :dp[j][pat[j]]
private:
    vector<vector<int>> dp;
public:
    void KMP(string pat) { // DP
        int m = pat.length();
        dp.resize(m, vector<int>(256, 0));//the total number of ASCII is 256
        dp[0][pat[0]] = 1;
        int X=0;
        for(int j=1; j<m; j++) {
            for(int c=0; c<256; c++) {
                if(c == pat[j]) {
                    dp[j][c] = j+1;
                } else {
                    dp[j][c] = dp[X][c];
                }
            }
            //update the shadow status X
            X = dp[X][pat[j]];
        }
    }
    int strStr(string haystack, string needle) {
        int m = needle.length(), n = haystack.length();
        if(m==0) return 0;
        KMP(needle);
        //use dp[][] to know how to transform in each status j
        int j = 0;
        for(int i=0; i<n; i++) {
            j = dp[j][haystack[i]];
            if(j==m) {
                return i-j+1;
            }
        }
        return -1;
    }
};