877. Stone Game

参考：https://labuladong.gitbook.io/algo/dong-tai-gui-hua-xi-lie/dong-tai-gui-hua-zhi-bo-yi-wen-ti

问题：

给定一堆石子的得分。A和B两个人进行如下游戏，

轮流，从石堆的两边选择一个石子，最终获得得分最大的人获胜。

由A先开始，求最终A是否能获胜。获胜则返回true，否则返回false。

Example 1:
Input: piles = [5,3,4,5]
Output: true
Explanation: 
Alex starts first, and can only take the first 5 or the last 5.
Say he takes the first 5, so that the row becomes [3, 4, 5].
If Lee takes 3, then the board is [4, 5], and Alex takes 5 to win with 10 points.
If Lee takes the last 5, then the board is [3, 4], and Alex takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alex, so we return true.
 

Constraints:
2 <= piles.length <= 500
piles.length is even.
1 <= piles[i] <= 500
sum(piles) is odd.

　　

解法：DP(动态规划)，math

解法一：DP

1.确定【状态】：石头堆 [ i ~ j ] 的

• 最左边石子：piles[i]
• 最右边石子：piles[j]

2.确定【选择】：对于先下的选手dp[i][j].first，分两种情况，取其中的最大值

• 选择最左边的石子：piles[i]
  • 现在的得分piles[i] + 去掉这个石子后剩下的石头堆 [ i+1 ~ j ] 中作为后下选手的最大得分 dp[i+1][j].second
  • 这时，对于后下的选手 dp[i][j].second =：
  • 只能从去掉这个石子后剩下的石头堆 [ i+1 ~ j ] 中，作为先下选手的最大得分 dp[i+1][j].first
• 选择最右边的石子：piles[j]
  • 现在的得分piles[j] + 去掉这个石子后剩下的石头堆 [ i ~ j-1 ] 中作为后下选手的最大得分 dp[i][j-1].second
  • 这时，对于后下的选手 dp[i][j].second =：
    • 只能从去掉这个石子后剩下的石头堆 [ i ~ j-1 ] 中，作为先下选手的最大得分 dp[i][j-1].first

3. dp[i][j]的含义：

将第 i 个石子到第 j 个石子最为对象石头堆，在这其中，所能获得的最大得分。

• dp[i][j].first：先下选手的最大得分。
• dp[i][j].second：后下选手的最大得分。

4. 状态转移：

dp[i][j].first = max {

• piles[i] + dp[i+1][j].second：选左边石子
  • 这时，dp[i][j].second = dp[i+1][j].first
• piles[j] + dp[i][j-1].second：选右边石子 }
  • 这时，dp[i][j].second = dp[i][j-1].first

5. base case：

• dp[i][i]：单石子堆
  • .first=piles[i]：先下选手得分就是该石子分值piles[i]。
  • .second=0：后下选手得分为0。（唯一石子已被先下选手拿走）

6. 遍历顺序：

根据状态转移公式，在求得dp[i][j]之前，需先求得dp[i+1][j]，dp[i][j-1]

 因此需要：i:大->小，j:小->大 遍历

 

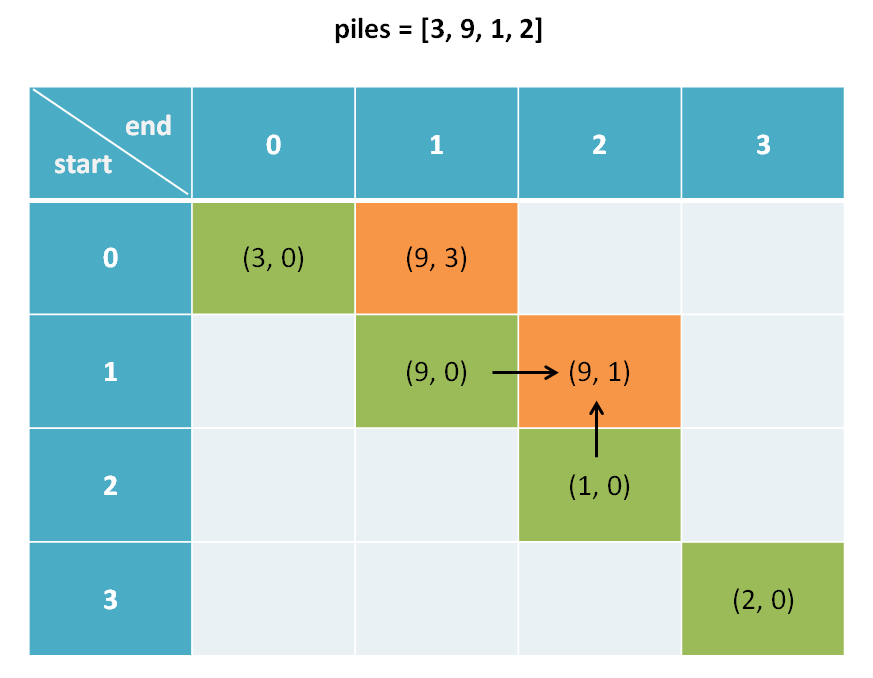
 代码参考：

class Solution {
public:
    //dp[i][j].first : among piles[i~j], the max points that the 1st player can get.
    //dp[i][j].second: among piles[i~j], the max points that the 2nd player can get.
    //for the 1st player:  dp[i][j].first = ?
    // case_1: choose piles[i]: = piles[i] + dp[i+1][j].second
    //       thus for the 2nd player can only choose from the left piles[i+1~j]
    //       dp[i][j].second = dp[i+1][j].first
    // case_2: choose piles[j]: = piles[j] + dp[i][j-1].second
    //       thus for the 2nd player can only choose from the left piles[i~j-1]
    //       dp[i][j].second = dp[i][j-1].first
    // base case:
    //       there is only one stone left.
    // dp[i][i].first = piles[i]
    // dp[i][i].second = 0
    // target:
    //       dp[0][size-1].first > dp[0][size-1].second
    bool stoneGame(vector<int>& piles) {
        int n = piles.size();
        vector<vector<pair<int, int>>> dp(n, vector<pair<int, int>>(n, pair<int,int>(0,0)));
        for(int i=0; i<n; i++) {
            dp[i][i].first = piles[i];
        }
        for(int i=n-2; i>=0; i--) {
            for(int j=i+1; j<n; j++) {
                int left = piles[i]+dp[i+1][j].second, right = piles[j]+dp[i][j-1].second;
                if(left >= right) {
                    dp[i][j].first = left;
                    dp[i][j].second = dp[i+1][j].first;
                } else {
                    dp[i][j].first = right;
                    dp[i][j].second = dp[i][j-1].first;
                }
            }
        }
        return dp[0][n-1].first > dp[0][n-1].second;
    }
};

♻️ 优化：

空间复杂度：2维->1维

去掉 i 

压缩所有行到一行。

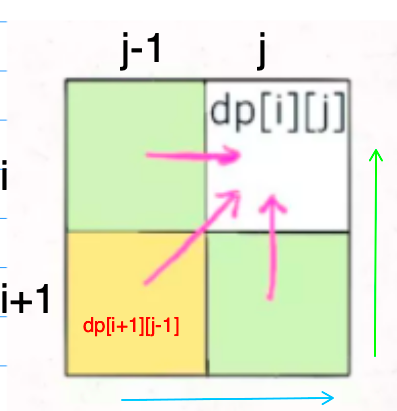
左下角dp[i+1][j-1]会被上面的dp[i][j-1]覆盖，因此引入变量pre，在更新dp[i][j-1]之前，保存dp[i+1][j-1]

 

比原先的这种赋值方式，少了黄色的方块区域，刚好不会存在需要的黄色区域被上方的绿色区域覆盖的情况。

 

因此直接去掉 i 即可。

⚠️ 注意：

1. 在初始化的时候，最开始的一行，和每一行（遍历 i）时的第一个元素dp[i]，需要首先初始化。（如下述代码L7～L11）

2. 本问题的first和second两个值的赋值先后问题需注意。（不要被覆盖：如下述代码L15～L18）

 

 

 代码参考：

class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        int n = piles.size();
        vector<pair<int, int>> dp(n, pair<int,int>(0,0));
        
        dp[n-1].first = piles[n-1];//initialize 1st row.
        dp[n-1].second = 0;
        for(int i=n-2; i>=0; i--) {
            dp[i].first = piles[i];//initialize 1st item of a row.
            dp[i].second = 0;
            for(int j=i+1; j<n; j++) {
                int left = piles[i]+dp[j].second, right = piles[j]+dp[j-1].second;
                if(left >= right) {
                    dp[j].second = dp[j].first;
                    //here *.first will be overwritten,
                    //so pay attention to the updating sequence of the pair.
                    dp[j].first = left;
                } else {
                    dp[j].first = right;
                    dp[j].second = dp[j-1].first;
                }
            }
        }
        return dp[n-1].first > dp[n-1].second;
    }
};

 

解法二：math

根据题目的限制条件：

• sum(piles) is odd.
• piles.length is even.

总共有偶数个石头堆，

石头总数为奇数。

即：对手双方可挑选的次数相同。

且，不可能存在打平的可能性。

 

而我作为先手。

则可选择我的所有选择：在奇数堆 or 偶数堆。

若我一旦选择了，即可控制在未来的所有选择中，都选择同一种类型的堆。

我只需要选择，石头和最大的那种堆即可。

 

解释：例如有 1，2，3，4 个堆

我先选择 1 or 4

选择 1：那么对方只能选择 2 or 4，这样的偶数堆。

选择 4: 那么对方只能选择 1 or 3，这样的奇数堆。

 

那么我一定可以赢。

返回 true 即可。

代码参考：

class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        return true; 
    }
};