516. Longest Palindromic Subsequence

问题：

给定一个字符串，求其中最长回文子序列（子序列不是连续字符串）的长度。

Example 1:
Input:
"bbbab"
Output:
4
One possible longest palindromic subsequence is "bbbb".
 
Example 2:
Input:
"cbbd"
Output:
2
One possible longest palindromic subsequence is "bb".
 
Constraints:
1 <= s.length <= 1000
s consists only of lowercase English letters.

　　

解法：DP(动态规划)

1.确定【状态】：字符串s的

• 第i个字符：s[i]
• 第j个字符：s[j]

2.确定【选择】：分两种情况

• s[i] == s[j]：
  • 前一个子串状态<不包含当前这两个字符s[i]s[j]>(公共序列长度)+2:  dp[i+1][j-1] + 2
• s[i] != s[j]：有以下2种情况，取最大值。
• 只有s[i]是最终最长回文子序列的一个字符    -> =上一个包含s[i]而不包含s[j]的字符状态：dp[i][j-1]
• 只有s[j]是最终最长回文子序列的一个字符   -> =上一个不包含s[i]而包含s[j]的字符状态：dp[i+1][j]
两个字符都不是最终最长回文子序列的一个字符 -> =上一个既不包含s[i]又不包含s[j]的字符状态：dp[i+1][j-1]
• ★由于dp[i+1][j-1]一定<=dp[i][j-1] or dp[i+1][j]，因此可以省略比较dp[i+1][j-1]

3. dp[i][j]的含义：

字符串s的第 i 个字符到第 j 个字符为止，这段子串中，存在最长回文子序列的长度。

4. 状态转移：

dp[i][j]=

• (s[i] == s[j])：=前一个子串状态+2：dp[i+1][j-1] + 2
• (s[i] != s[j])：=max {
  • 上一个包含s[i]字符的状态：dp[i][j-1]
  • 上一个包含s[j]字符的状态：dp[i+1][j]
  • 上一个s[i]s[j]都不包含的状态：dp[i+1][j-1]（★可省略）    }

5. base case：

• dp[i][i]=1：单文字子串，最长回文子序列为它自己，长度为 1。

6. 遍历顺序：

根据状态转移公式，在求得dp[i][j]之前，需先求得dp[i+1][j-1]，dp[i+1][j]，dp[i][j-1]

 因此需要：i:大->小，j:小->大 遍历

 

⚠️ 注意：本问题，i一定<=j，因此dp[i][j]中i>j的memory基本不会被用到。

只有在base case计算dp[i][i+1]且s[i]==s[i+1]的时候，作为★dp[i+1][j-1]被用到。应该为0。这也是在后面♻️ 优化处pre的赋值理由。

 

代码参考：

class Solution {
public:
    //dp[i][j]: in substring: s[i~j], the length of LPS.
    //case_1: s[i]==s[j]:dp[i+1][j-1] + 2
    //        add 2 to the pre status(which both not include s[i]s[j]) dp[i+1][j-1]
    //case_2: s[i]!=s[j]: max of following 2 case:
    //        case_2_1: the pre status(only include s[i],s[i] is in LPS). dp[i][j-1]
    //        case_2_2: the pre status(only include s[j],s[j] is in LPS). dp[i+1][j]
    //base case:
    //dp[i][i]:1
    int longestPalindromeSubseq(string s) {
        int n = s.length();
        vector<vector<int>> dp(n, vector<int>(n, 0));
        for(int i=0; i<n; i++) {
            dp[i][i] = 1;
        }
        for(int i=n-1; i>=0; i--) {
            for(int j=i+1; j<n; j++) {
                if(s[i]==s[j]) {
                    dp[i][j] = dp[i+1][j-1] +2;
                } else {
                    dp[i][j] = max(dp[i][j-1], dp[i+1][j]);
                }
            }
        }
        return dp[0][n-1];
    }
};

♻️ 优化：

空间复杂度：2维->1维

去掉 i 

压缩所有行到一行。

左下角dp[i+1][j-1]会被上面的dp[i][j-1]覆盖，因此引入变量pre，在更新dp[i][j-1]之前，保存dp[i+1][j-1]

 

 

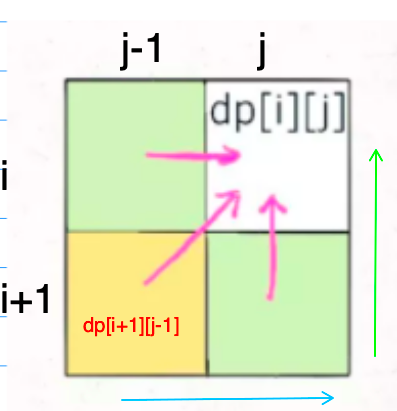
代码参考：

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.length();
        vector<int> dp(n, 0);
        for(int i=n-1; i>=0; i--) {
            int pre = 0;
            //base case:for s[i~i+1]->e.g.'aa',s[i]=s[j]->dp[j]=pre+2 (should)=2->pre=0
            dp[i] = 1;//base case
            for(int j=i+1; j<n; j++) {
                int tmp = dp[j];
                if(s[i]==s[j]) {
                    dp[j] = pre +2;
                } else {
                    dp[j] = max(dp[j-1], dp[j]);
                }
                pre = tmp;
            }
        }
        return dp[n-1];
    }
};