312. Burst Balloons

参考：https://mp.weixin.qq.com/s/I0yo0XZamm-jMpG-_B3G8g

问题：

给定一组气球藏有的金币数。若戳破一个气球，则可得其相邻两个气球和自己藏有金币之积。

求按一定顺序戳破气球，最终能获得最多金币是多少。

Note:
You may imagine nums[-1] = nums[n] = 1. They are not real therefore you can not burst them.
0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100

Example:
Input: [3,1,5,8]
Output: 167 
Explanation: nums = [3,1,5,8] --> [3,5,8] -->   [3,8]   -->  [8]  --> []
             coins =  3*1*5      +  3*5*8    +  1*3*8      + 1*8*1   = 167

　　

解法：DP(动态规划)

1.确定【状态】：

由于本问题中，戳破某一个气球，与其前后相邻的两个气球有关，而这两个相邻气球会根据戳破决策（戳破气球顺序）变化。因此

• 相邻左边的气球：i
• 相邻右边的气球：j

 

 

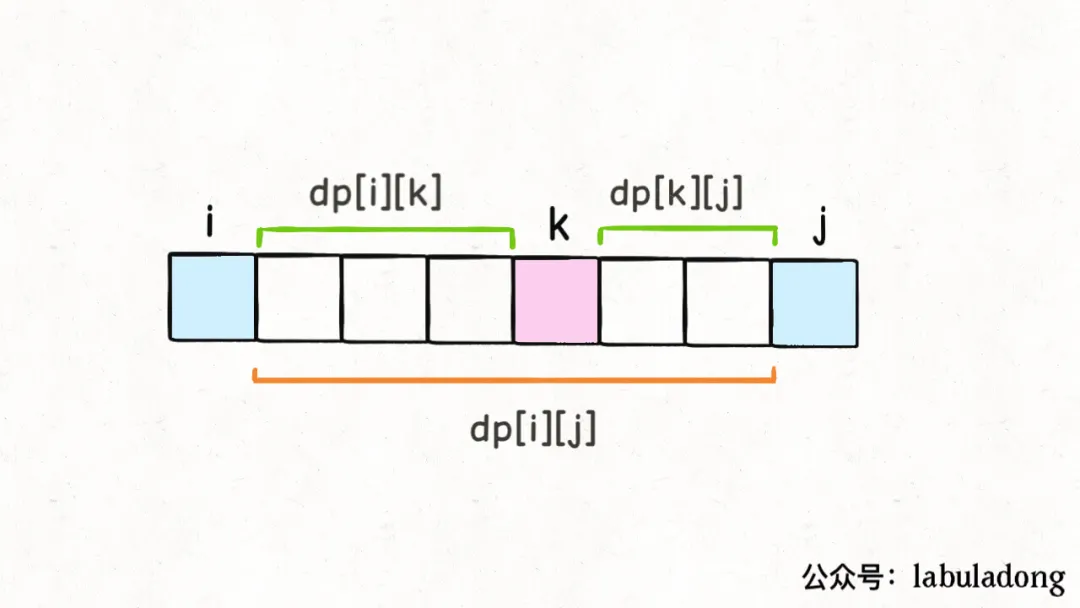
2.确定【选择】：

• 选择max（k=[i+1～j-1]，中任意的一个气球，最后一个戳破它，可使得金币最多）：气球k

3. dp[i][j]的含义：

从第i+1～j-1中，选取最后一个气球k戳破，所得到最多的金币数。

4. 状态转移：

dp[i][j]= max {

• dp[i][k] + dp[k][j] + coins[i]*coins[k]*coins[j]。
• 先戳破k之前的气球所得最大 + 先戳破k之后的气球所得最大 + 最后戳破k：最后只剩下k和其前后相邻气球i，j。

}

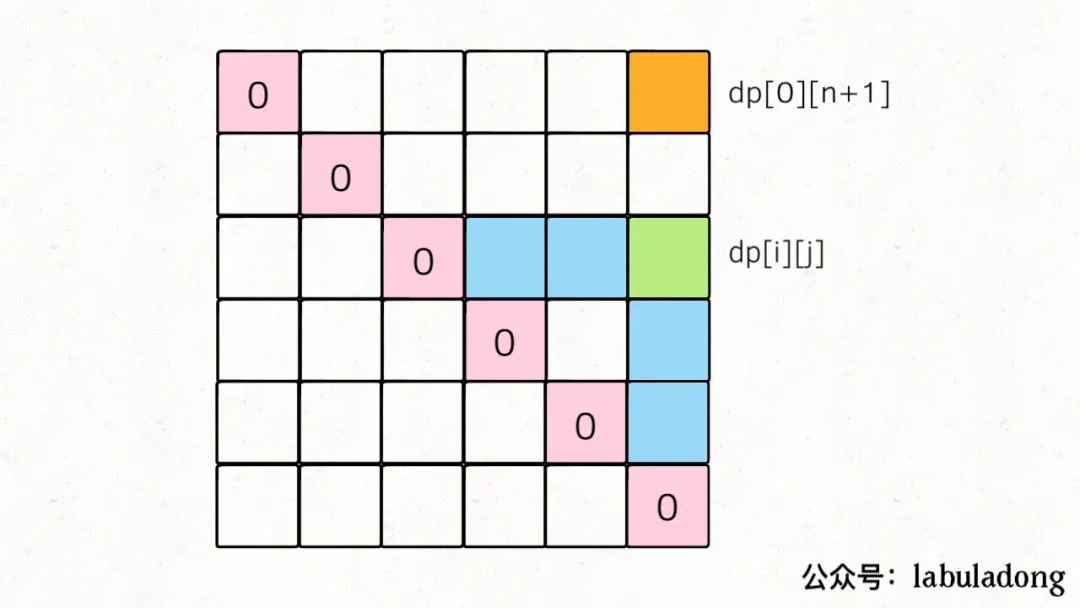
5. base case：

• dp[i][i]=0
• dp[i][i+1]=0

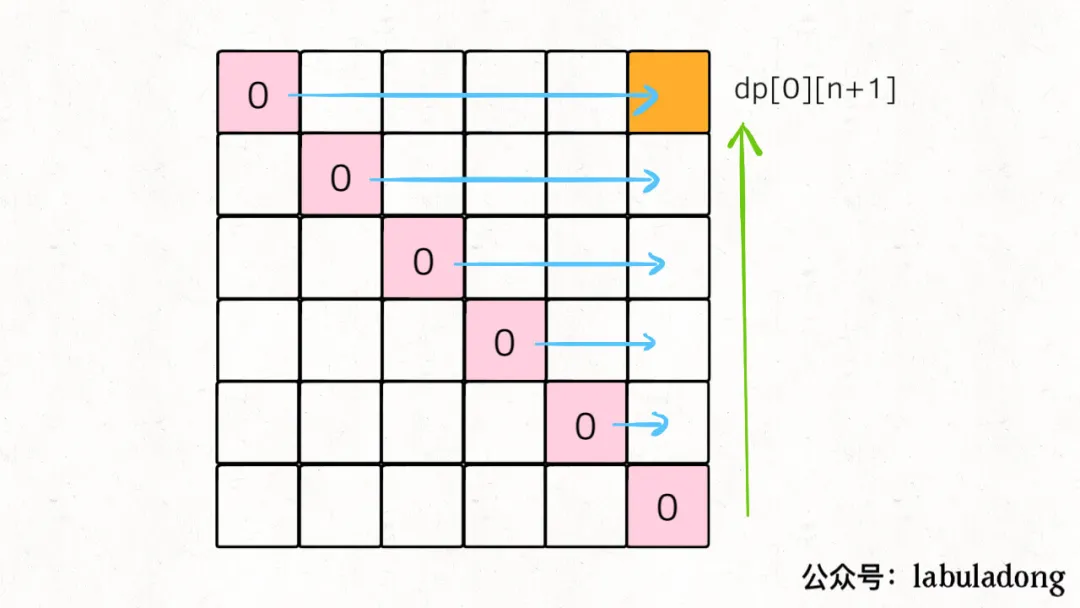
6. 遍历顺序：

根据状态转移公式，在求得dp[i][j]之前，需先求得dp[i][k]，dp[k][j]

 

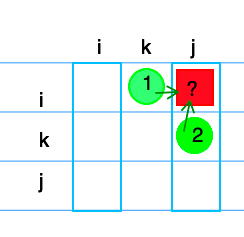
 因此需要：i:大->小，j:小->大 遍历

 

 

 

 

代码参考：

class Solution {
public:
    //dp[i][j]:in i~j-th balloons，last step is to break k-th balloon to let us get the max coins.
    //find k-th ballon, k:i+1~j-1  ->  i<=j-2
    //max{
    //  dp[i][k] + dp[k][j] + nums[k]*nums[i]*nums[j]
    //}
    //base case:
    //  dp[i][i] = 0
    //  dp[i][i+1] = 0
    int maxCoins(vector<int>& nums) {
        int n = nums.size();
        vector<int> coins(n+2,1);//except coins[0], coins[n+1];
        for(int i=0; i<n; i++) {
            coins[i+1] = nums[i];
        }
        vector<vector<int>> dp(n+2, vector<int>(n+2, 0));//0~n+1
        for(int i=n; i>=0; i--) {
            for(int j=i+2; j<n+2; j++) {
                for(int k=i+1; k<=j-1; k++) {
                    dp[i][j] = max(dp[i][j], dp[i][k]+dp[k][j]+coins[k]*coins[i]*coins[j]);
                }
            }
        }
        return dp[0][n+1];
    }
};