72. Edit Distance

参考：https://labuladong.gitbook.io/algo/dong-tai-gui-hua-xi-lie/zhuang-tai-ya-suo-ji-qiao

问题：

给定两个字符串，求出由一个字符串转化为另一个字符串的最短编辑距离。（编辑操作次数）

有以下三种编辑：

• 插入
• 删除
• 替换

Example 1:
Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation: 
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')

Example 2:
Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation: 
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')

　　

解法：DP(动态规划)

1.确定【状态】：

• 字符串S1的第i个字符：word1[i]
• 字符串S2的第j个字符：word2[j]

2.确定【选择】：分两种情况

• word1[i] == word2[j]：操作数不变
  • 不做任何操作，继续比较两字符串的下一个字符：i++，j++
• word1[i] != word2[j]：以下三种操作之一，操作数+1
  • 插入操作：给word1[i]之前，插入word2[j] -> 那么下一次比较 i（不动），j++（j的下一位）
  • 删除操作：删除word1[i]                        -> 那么下一次比较 i（i的下一位），j（不动）
  • 替换操作：将word1[i]替换成word2[j]       -> 那么继续比较两字符串的下一位：i++，j++

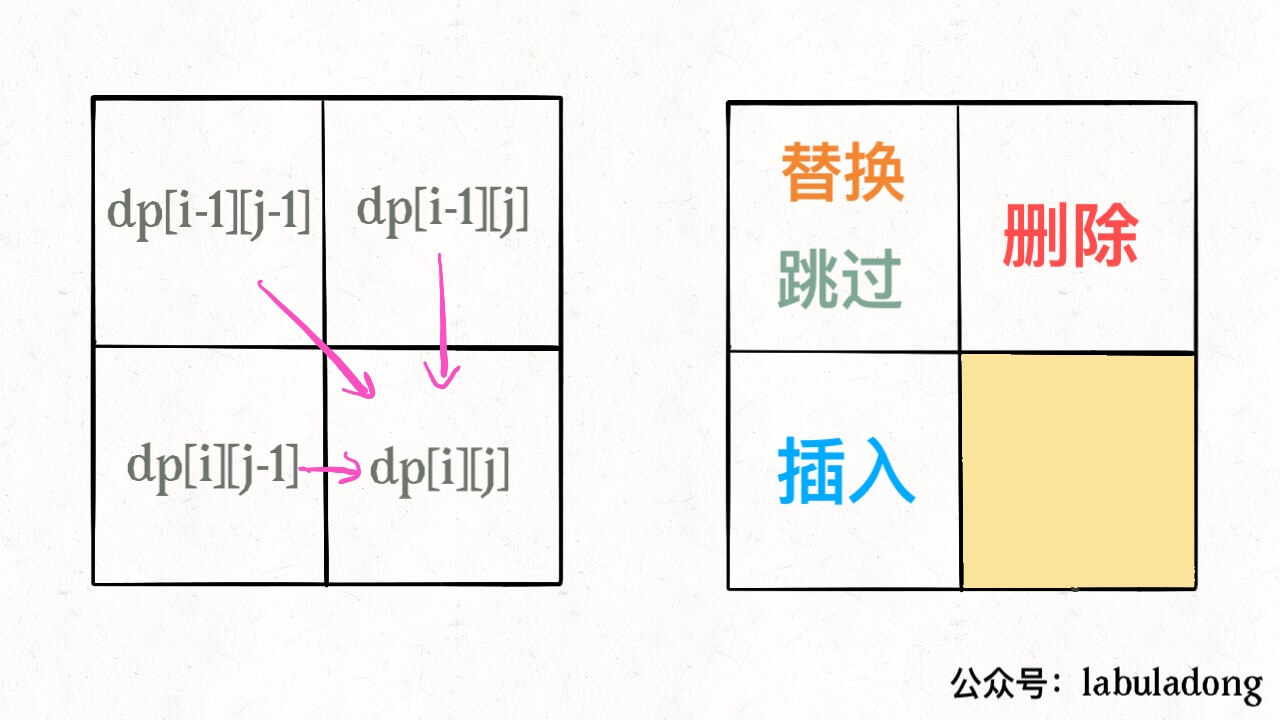
3. dp[i][j]的含义：

对比到word1的第 i 个字符，word2的第 j 个字符，使得两个字符串相同，所做的最少编辑次数。

4. 状态转移：

dp[i][j]=

• (word1[i] == word2[j])：=上一个状态的次数：dp[i-1][j-1]
• (word1[i] != word2[j])：=min {
  • 上一个状态，通过：插入操作 得到：dp[i][j-1] + 1
  • 上一个状态，通过：删除操作 得到：dp[i-1][j] + 1
  • 上一个状态，通过：替换操作 得到：dp[i-1][j-1] + 1    }

5. base case：

• dp[0][j]=j：S1始终在第0位上，要通过 j 步插入操作，才能与S2到第 j 位一致。
• dp[i][0]=i：S2始终在第0位上，S1要通过 i 步删除操作，才能与S2到第 0 位一致。

代码参考：

class Solution {
public:
    //dp[i][j]:until s1[i],s[j],the minimal steps has been taken to make two words same.
    //case_1: s1[i]==s2[j]: =dp[i-1][j-1]
    //case_2: s1[i]!=s2[j]: min(case_2_1, case_2_2, case_2_3)
    //       case_2_1:insert-> =dp[i][j-1]+1 // s1[i] insert s2[j], 
                                           //then next comparation is -> i stop, j+1
    //       case_2_2:delete-> =dp[i-1][j]+1 // s1[i] delete, 
                                           //then next comparation is -> i+1, j stop
    //       case_2_3:replace-> =dp[i-1][j-1]+1 // s1[i] replace to s2[j], 
                                           //then next comparation is -> i+1, j+1
    //base case:
    //dp[i][0]=i
    //dp[0][j]=j
    int minDistance(string word1, string word2) {
        int m=word1.length(), n=word2.length();
        vector<vector<int>> dp(m+1, vector<int>(n+1, 0));
        for(int i=0; i<=m; i++) dp[i][0]=i;
        for(int j=0; j<=n; j++) dp[0][j]=j;
        
        for(int i=1; i<=m; i++) {
            for(int j=1; j<=n; j++) {
                if(word1[i-1]==word2[j-1]) {
                    dp[i][j] = dp[i-1][j-1];
                } else {
                    dp[i][j] = min(dp[i][j-1]+1, dp[i-1][j]+1);
                    dp[i][j] = min(dp[i][j], dp[i-1][j-1]+1);
                }
            }
        }
        return dp[m][n];
    }
};

♻️ 优化：

空间复杂度：2维->1维

去掉 i 

压缩所有行到一行。

左上角dp[i-1][j-1]会被下面的dp[i][j-1]覆盖，因此引入变量pre，在更新dp[i][j-1]之前，保存dp[i-1][j-1]

⚠️ 注意：在每一行最开始的初始化，也要注意pre要初始化为每一行上一行的开头元素dp[i][0]=i

 

代码参考：

class Solution {
public:
    //dp[i][j]:until s1[i],s[j],the minimal steps has been taken to make two words same.
    //case_1: s1[i]==s2[j]: =dp[i-1][j-1]
    //case_2: s1[i]!=s2[j]: min(case_2_1, case_2_2, case_2_3)
    //       case_2_1:insert-> =dp[i][j-1]+1 // s1[i] insert s2[j], 
                                           //then next comparation is -> i stop, j+1
    //       case_2_2:delete-> =dp[i-1][j]+1 // s1[i] delete, 
                                           //then next comparation is -> i+1, j stop
    //       case_2_3:replace-> =dp[i-1][j-1]+1 // s1[i] replace to s2[j], 
                                           //then next comparation is -> i+1, j+1
    //base case:
    //dp[i][0]=i
    //dp[0][j]=j
    int minDistance(string word1, string word2) {
        int m=word1.length(), n=word2.length();
        vector<int> dp(n+1, 0);
        for(int j=0; j<=n; j++) dp[j]=j;
        
        for(int i=1; i<=m; i++) {
            int pre=dp[0];//pre line's first item
            dp[0] = i;//dp[i][0]=i
            for(int j=1; j<=n; j++) {
                int tmp = dp[j];
                if(word1[i-1]==word2[j-1]) {
                    dp[j] = pre;
                } else {
                    dp[j] = min(dp[j-1]+1, dp[j]+1);
                    dp[j] = min(dp[j], pre+1);
                }
                pre = tmp;
            }
        }
        return dp[n];
    }
};