218. The Skyline Problem

问题：

给定一个数组，表示楼的宽+高[x1,x2,h]，求所形成的城市轮廓。

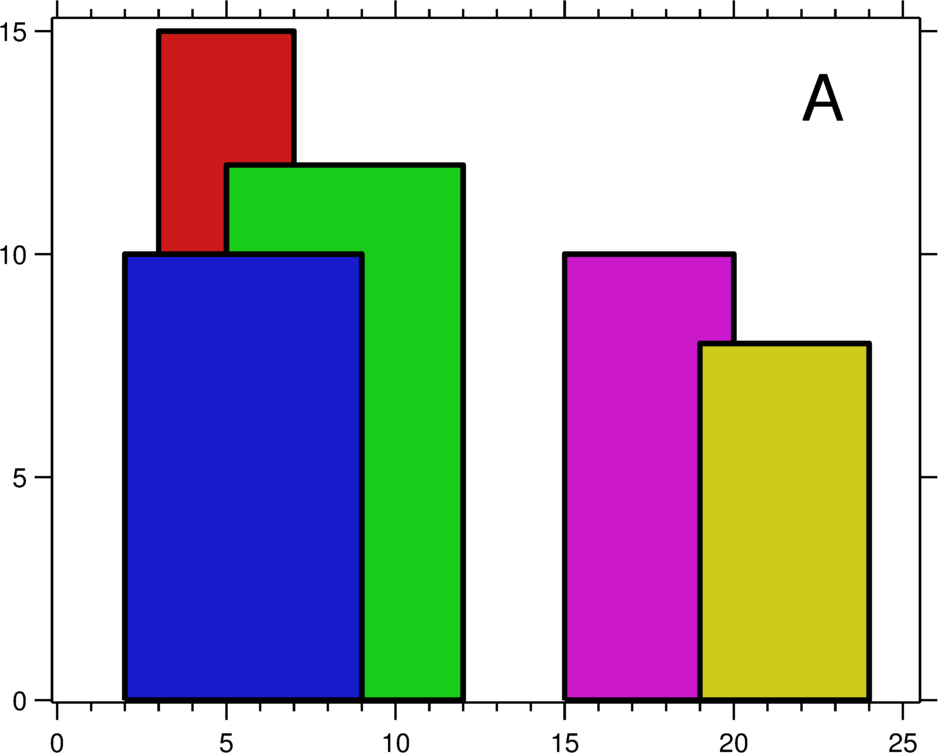
Input
[[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
Output
[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]

Input
[[1,2,1],[1,2,2],[1,2,3]]
Output
[[1,3],[2,0]]

　　

解法：

解法一：FenwickTree

利用特点：通常的FenwickTree（如下图）所求为，前0～i个元素的和。

前面的值 贡献构成->后面的值

 

 

 

这里，我们利用后缀构造，求第i～∞个元素中的最大值。

后面的值(x2) 贡献构成->前面的值(x1~x2之间的值)。

• index：x2
• value：max(h)

 

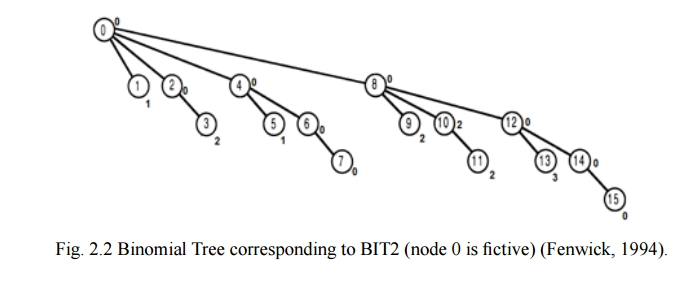
 例如，上图中

• tree[2]：表示node[2]的最大值和node[3]的最大值，再求最大值。
• tree[8]：表示node[8]，node[9]...node[15]的最大值。

在本问题中，我们每读入一个楼的信息（遍历到x1的位置时），[x1,x2,h] 将上述的数据结构 update(x2, h)

更新node[x2]上的值，同时更新<x2的idx上的各个node的值。

• 当我们求，x0的最大值时，还未录入h，x0累计>x0的各个值。由于刚开始所以都为0
• 当我们求，x1.5的最大值时，已录入h，x1.5累计>x1.5的各个值，包含x2。因此为h
• 当我们求，x3的最大值时，x3累计>x3的各个值，不包含x2，因此h不能参与计算。

 

代码参考：

class FenwickTree {//Suffix sum tree (Normal is Preffix sum tree)
public:
    FenwickTree(int n):tree(n+1, 0) {}
    void update(int i, int delta) {
        i++;
        while(i>=1){
            tree[i]=max(tree[i], delta);
            i -= lowbit(i);
        }
    }
    int getSuMax(int i) {//max(i~infinite)
        int maxres = 0;
        i++;
        while(i<tree.size()){
            maxres=max(tree[i], maxres);
            i += lowbit(i);
        }
        return maxres;
    }
    
private:
    vector<int> tree;
    int lowbit(int x) {
        return x&(-x);
    }
};

class Event {
public:
    int x;//坐标x
    int h;//高度
    int i;//楼号
};

class Solution {
public:
    static bool cmp(Event a, Event b){
        return (a.x == b.x)? a.h > b.h : a.x < b.x;//x坐标相同的情况下，高的排前面（防止二重输出）
    }
    vector<vector<int>> getSkyline(vector<vector<int>>& buildings) {
        set<vector<int>> res;
        vector<Event> eventlist;
        map<int,int> posX;//映射x2排序后的index
        int i=0, j=0;
        for(vector<int> b:buildings){
            eventlist.push_back({b[0], b[2], j});//楼开始
            eventlist.push_back({b[1], -b[2], j++});//楼结束
        }
        sort(eventlist.begin(), eventlist.end(), cmp);
        for(int i=0; i<eventlist.size(); i++){
            posX.insert({eventlist[i].x, i});
        }
        FenwickTree ftree(eventlist.size());
        for(Event e:eventlist){
            int maxh = ftree.getSuMax(posX[e.x]);//FenwickTree query
            if(e.h > 0) {
                int x2 = buildings[e.i][1];
                ftree.update(posX[x2], e.h);//FenwickTree update
                if(abs(e.h) > maxh) res.insert({e.x, e.h});
            } else {
                int maxh2 = ftree.getSuMax(posX[e.x]+1);
                if(abs(e.h) > maxh2) res.insert({e.x, maxh2});
            }
        }
        vector<vector<int>> res1(res.begin(), res.end());//去重
        return res1;
    }
};

 

解法二：multiset

【参考 huahua：https://zxi.mytechroad.com/blog/tree/leetcode-218-the-skyline-problem/】

利用multiset的特性：

• insert形成排好序的set，最小值begin()，最大值rbegin()
• 允许重复元素

我们需要用到的操作：

• 插入一个数，insert(val) 
• 删除某个值，erase(find(val))
• 最大值，*rbegin()
• 最小值，*begin()

插入一个数，删除一个数：时间复杂度：O(logn)

⚠️ 注意：

由于避免向结果插入多余不必要的节点，我们使用eventlist排序时，

1. 首先按照x坐标排序，其次若x相同，则大楼 entering事件 先于 leave事件 处理。
2. 若都是entering事件，那么更高的楼先处理。

因此有：

    static bool cmp(Event a, Event b){
        return (a.x == b.x)? a.h > b.h : a.x < b.x;
    }

    sort(eventlist.begin(), eventlist.end(), cmp);

理由如下2图：

 

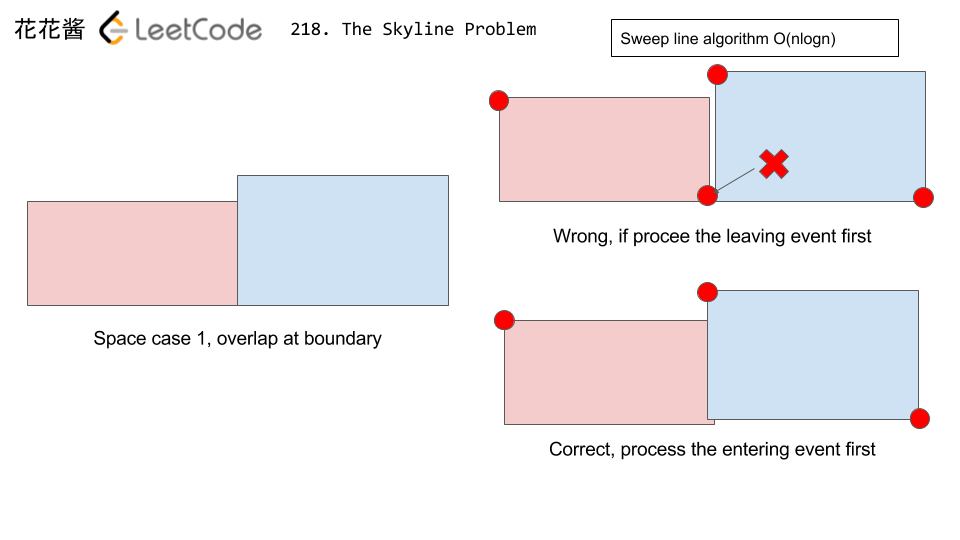
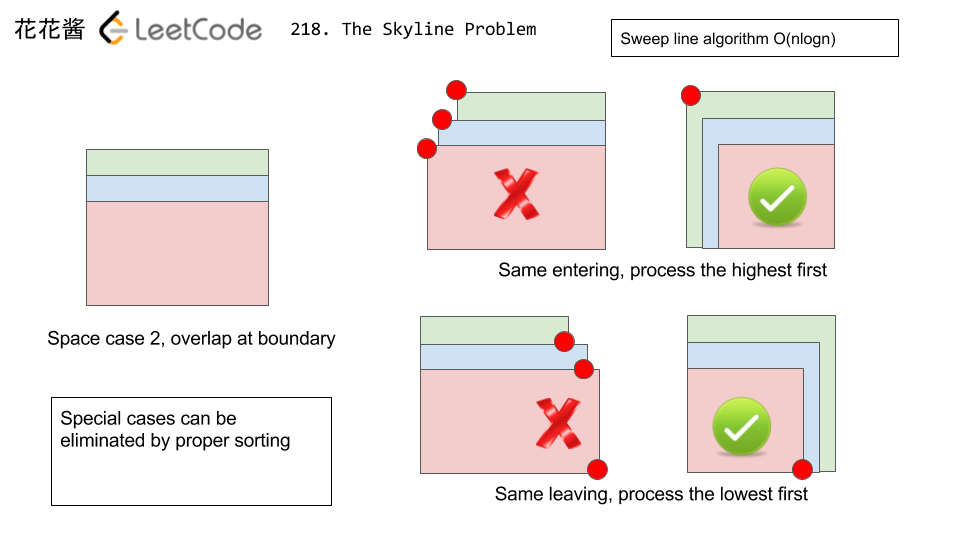
代码参考：

class Event {
public:
    int x;
    int h;
};

class Solution {
public:
    static bool cmp(Event a, Event b){
        return (a.x == b.x)? a.h > b.h : a.x < b.x;
    }
    vector<vector<int>> getSkyline(vector<vector<int>>& buildings) {
        vector<vector<int>> res;
        vector<Event> eventlist;
        for(vector<int> b:buildings){
            eventlist.push_back({b[0], b[2]});
            eventlist.push_back({b[1], -b[2]});
        }
        sort(eventlist.begin(), eventlist.end(), cmp);
        for(Event e:eventlist){
            bool entering = e.h>=0;
            int newh = abs(e.h);
            int maxh;
            if(entering){
                maxh = getMaxHeight();
                if(newh>maxh){
                    res.push_back({e.x, newh});
                }
                height.insert(newh);
            }else{
                height.erase(height.find(newh));
                maxh = getMaxHeight();
                if(maxh<newh){
                    res.push_back({e.x, maxh});
                }
            }
        }
        return res;
    }
private:
    multiset<int> height;
    int getMaxHeight(){
        if(height.size()==0) return 0;
        else return *height.rbegin();
    }
};