1260. Shift 2D Grid

问题：

给定一个二维数组，

对二维数组进行以下变化：

• 按列（头尾循环）向右平移1位
• 对第一列，按行（头尾循环）向下平移1位。

对数组做K次以上操作。求得到的新数组。

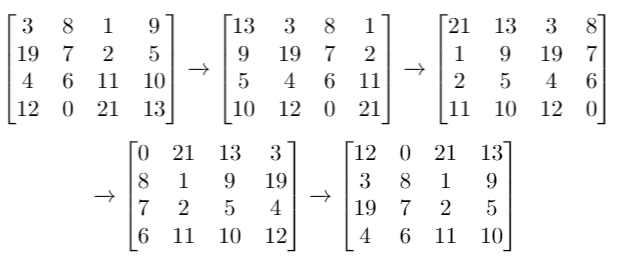
Example 1:
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2:
Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3:
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]
 

Constraints:
m == grid.length
n == grid[i].length
1 <= m <= 50
1 <= n <= 50
-1000 <= grid[i][j] <= 1000
0 <= k <= 100

 

 

 

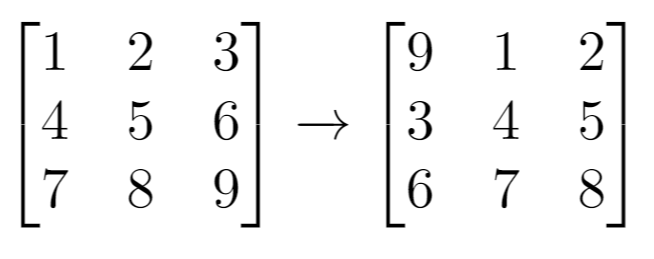
解法：

列数平移K位，那么原来的第j列，将被移到，(j+K)%列数

第一列会被平移行数K位，那么原来的第i行第j列的元素，离第一列的距离位：j，那么它会被移动行数为：(i+(j+K)%列数)%行数

 

下面代码：列数=n，行数=m

代码参考：

class Solution {
public:
    vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {
        int m=grid.size(), n=grid[0].size();
        int col=k%n;
        vector<vector<int>> res(grid);
        for(int i=0; i<m; i++){
            for(int j=0; j<n; j++){
                res[(i+(j+k)/n)%m][(j+col)%n]=grid[i][j];
            }
        }
        return res;
    }
};

 

另外一种方法：

每一个元素[i,j]看作一个数，值为：i*列数+j

进制为：列数

上述的移动操作，可以看作是，

对于每一个值进行+1操作，而到第一列的时候，该进位，刚好也满足+1的操作。

因此，每一个元素经过K次操作，即为：value=i*列数+j+K

而最终所处的位置即是：[value/列数][value%列数]

⚠️ 注意：由于数组为循环移动，所以整个数组有时以 列数*行数 为一循环。

因此在得出value的时候，需要 %列数*行数 取模。

 

代码参考：

class Solution {
public:
    vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {
        int m=grid.size(), n=grid[0].size();
        vector<vector<int>> res(grid);
        for(int i=0; i<m; i++){
            for(int j=0; j<n; j++){
                int value=(i*n+j+k)%(m*n);
                res[value/n][value%n]=grid[i][j];
            }
        }
        return res;
    }
};