1252. Cells with Odd Values in a Matrix

问题：

给定矩阵尺寸n*m，矩阵初始化为全为0，

和操作对象行列数组，indices[i] = [ri, ci]

对这些行列，依次+1。

求最终得到的矩阵中有多少个元素为奇数。

Example 1:
Input: n = 2, m = 3, indices = [[0,1],[1,1]]
Output: 6
Explanation: Initial matrix = [[0,0,0],[0,0,0]].
After applying first increment it becomes [[1,2,1],[0,1,0]].
The final matrix will be [[1,3,1],[1,3,1]] which contains 6 odd numbers.

Example 2:
Input: n = 2, m = 2, indices = [[1,1],[0,0]]
Output: 0
Explanation: Final matrix = [[2,2],[2,2]]. There is no odd number in the final matrix.
 
Constraints:
1 <= n <= 50
1 <= m <= 50
1 <= indices.length <= 100
0 <= indices[i][0] < n
0 <= indices[i][1] < m

 

 

 

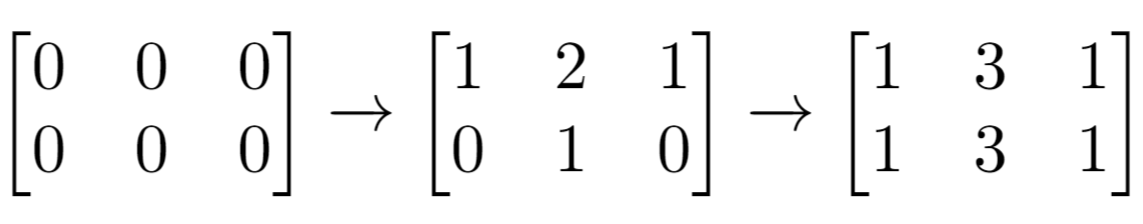
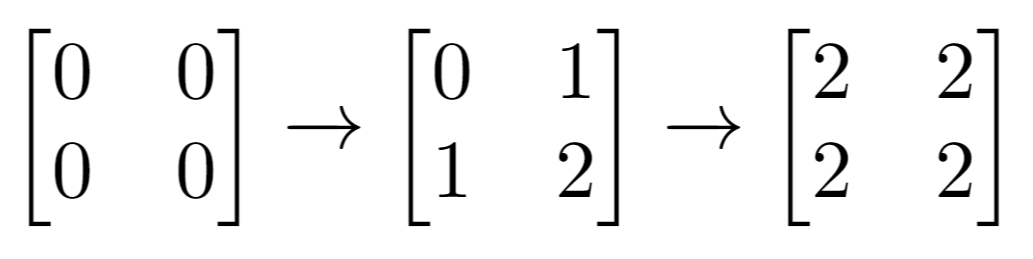
解法：

由于本问题，只涉及奇偶性，则我们可以考虑使用1，0表示

这里我们用到 bitset 结构。

首先根据限制条件，我们初始化最大为50的

row和col的bitset

（⚠️ 注意：bitset无法动态初始化）

根据给定的 操作对象行列数组，indices[i] = [ri, ci]

对row[ri]，col[ci]累计

由于本题只在乎奇偶性，则从初始的0开始，累计计算

则是奇偶轮询变化，即可使用flip函数实现。

 

然后我们最终得到所有行变化，列变化后的结果。

我们使用这个结果，对row*col的矩阵每一个元素，进行奇偶性判断

如，元素[r1,c1]的奇偶性则为：row[r1]+col[c1]的奇偶性。

而我们最终所要得到的是 值为奇数的元素个数。

这里可以使用bitset的count方法，直接得到所含1的位数。

那么，我们对每一行，

如果该行row[i]为1，那么整行的奇数元素个数为：col中所含偶数的个数：size-count

如果该行row[i]为0，那么整行的奇数元素个数为：col中所含奇数的个数：count

奇+偶=奇

偶+奇=奇

 

代码参考：

class Solution {
public:
    int oddCells(int n, int m, vector<vector<int>>& indices) {
        bitset<50> row, col;
        int res=0;
        for(auto ind:indices){
            row[ind[0]].flip();
            col[ind[1]].flip();
        }
        for(int i=0; i<n; i++){
            if(row[i]==0) res+=col.count();
            else res+=(m-col.count());
        }
        return res;
    }
};