1222. Queens That Can Attack the King

问题：

给定8*8棋盘中，queen的坐标，和king的坐标。

king的同一行，同一列，同一对角线上的第一个queen，为可攻击king的queen

求所有可攻击king的queen的坐标数组。

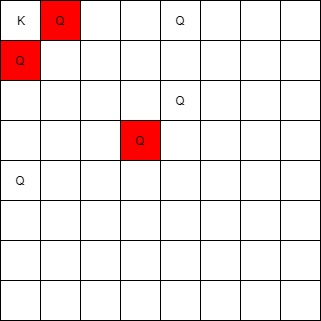
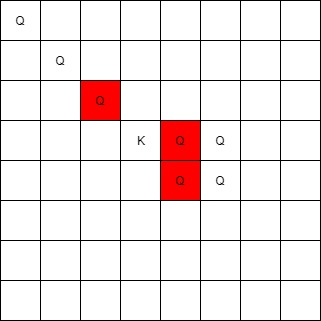
Example 1:
Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
Output: [[0,1],[1,0],[3,3]]
Explanation:  
The queen at [0,1] can attack the king cause they're in the same row. 
The queen at [1,0] can attack the king cause they're in the same column. 
The queen at [3,3] can attack the king cause they're in the same diagnal. 
The queen at [0,4] can't attack the king cause it's blocked by the queen at [0,1]. 
The queen at [4,0] can't attack the king cause it's blocked by the queen at [1,0]. 
The queen at [2,4] can't attack the king cause it's not in the same row/column/diagnal as the king.

Example 2:
Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
Output: [[2,2],[3,4],[4,4]]

Example 3:
Input: queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
Output: [[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]
 
Constraints:
1 <= queens.length <= 63
queens[0].length == 2
0 <= queens[i][j] < 8
king.length == 2
0 <= king[0], king[1] < 8
At most one piece is allowed in a cell.

　　        

 

 

 

解法：

一共有8个方向，可作为要求的queen

分别为：king 的右方→，左方←，下方↓，上方↑，左上↖️，右上↗️，左下↙️，右下↘️。

那么构建待选数组cand

vector<vector<int>> cand={{0,1},{0,-1},{1,0},{-1,0},{1,1},{-1,-1},{1,-1},{-1,1}};

将所有待选queens放入unordered_set中方便查找。

分别试探以king为起始，向8个方向逐次+1距离的节点，是否在queens里面。

在的话，加入res。

 

代码参考：

class Solution {
public:
    vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {
        vector<vector<int>> cand={{0,1},{0,-1},{1,0},{-1,0},{1,1},{-1,-1},{1,-1},{-1,1}};
        unordered_set<int> qs;
        vector<vector<int>> res;
        for(vector<int> queen:queens){
            qs.insert(queen[0]*8+queen[1]);
        }
        for(int i=0; i<8; i++){
            int x=king[0], y=king[1];
            while(x>=0 && x<8 && y>=0 && y<8){
                if(qs.find(x*8+y)!=qs.end()){
                    res.push_back({x,y});
                    break;
                }
                x+=cand[i][0];
                y+=cand[i][1];
            }
        }
        return res;
    }
};