1007. Minimum Domino Rotations For Equal Row

问题：

给两个由[1~6]之间的数字构成的两个数组A，B

若对其中一个数组中的一些元素用另一个数组同样index的元素替换，使得这个数组的所有元素都相同，

求最小替换个数。

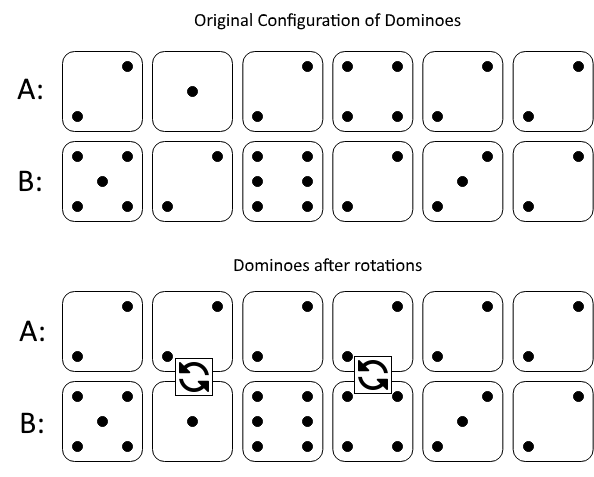
Example 1:
Input: A = [2,1,2,4,2,2], B = [5,2,6,2,3,2]
Output: 2
Explanation: 
The first figure represents the dominoes as given by A and B: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.

Example 2:
Input: A = [3,5,1,2,3], B = [3,6,3,3,4]
Output: -1
Explanation: 
In this case, it is not possible to rotate the dominoes to make one row of values equal. 

Note:
1 <= A[i], B[i] <= 6
2 <= A.length == B.length <= 20000

　　

解法1：

我们提出第一组元素A[0]B[0]，

如果能成功进行替换操作，那么要被替换成的数字一定在A[0]orB[0]之间产出。

否则，则两个数字都不满足条件，那么我们直接返回-1即可。

 

在满足条件的情况下，

假设A[0]是那个目标元素。

那么，对所有A[i]和B[i]，进行判断如果!=A[0]，需要替换的次数分别为a,b

遍历完后，取A和B的替换次数a，b的最小值即可。

同样的，如果B[0]是那个目标元素。

也同样对

所有A[i]和B[i]，进行判断如果!=A[0]，需要替换的次数分别为a,b

遍历完后，取A和B的替换次数a，b的最小值即可。

 

代码参考：

class Solution {
public:
    int minDominoRotations(vector<int>& A, vector<int>& B) {
        int n=A.size();
        for(int i=0, a=0, b=0; (A[i]==A[0] || B[i]==A[0]) && i<n; i++){
            if(A[i]!=A[0]) a++;
            if(B[i]!=A[0]) b++;
            if(i==n-1) return min(a,b);
        }
        for(int i=0, a=0, b=0; (A[i]==B[0] || B[i]==B[0]) && i<n; i++){
            if(A[i]!=B[0]) a++;
            if(B[i]!=B[0]) b++;
            if(i==n-1) return min(a,b);
        }
        return -1;
    }
};

 

解法2:

依次对A和B进行累计每个元素出现的个数。和同一位置同时出现的个数same

元素的取值范围只能是1，2，3，4，5，6

所以使用数组coutA[7] ，coutB[7]，same[7]即可

按照题意，最终我们需要将A或者B全部置为元素X

那么，对于元素X，

（A中的个数 + B中的个数 = 各自单独存在的个数 + 2*同时存在的个数）

在A中的个数 + 在B中的个数 - 同时存在的个数

= 两者不同时存在的个数 + 同时存在的个数

应该 = 总位数A.size

所以，对所有满足上述计算结果的元素X，求

A中需要替换的次数：size-coutA[X]

B中需要替换的次数：size-coutB[X]

二者的最小值。

然后在所有的结果中再求最小。

 

代码参考：

class Solution {
public:
    int minDominoRotations(vector<int>& A, vector<int>& B) {
        int res=INT_MAX;
        int coutA[7]={0}, coutB[7]={0}, same[7]={0};
        int n=A.size();
        for(int i=0; i<n; i++){
            coutA[A[i]]++;
            coutB[B[i]]++;
            if(A[i]==B[i])same[A[i]]++;
        }
        for(int i=1; i<7; i++){
            if(coutA[i]+coutB[i]-same[i]==n){
                res=min(res, min(n-coutA[i],n-coutB[i]));
            }
        }
        if(res>n) return -1;
        return res;
    }
};