算法分析与设计(work11)

1、问题

给定字符集 \(C =\{x_{1},x_{2},...,x_{n}\}\) 和每个字符的频率 \(f(x_{i})\) ，求关于C的 一个最优前缀码？

2、解析

构造一个最优前缀码的贪心方法就是哈夫曼算法（Huffman)。
因为二元前缀编码的储存就是就是二叉树结构，每个字符作为树叶，对应这个字符的前缀码看作根到这片树叶的一条路径，每个结点通向左二子的边记作 0，通向右儿子的边记作 1.
那么这个问题我们可以进行一下转化，问题就是构造一颗带权的二叉树，使得各个叶子节点x的深度乘以出现的频率f(x) 之和最小。
很显然考虑贪心算法，即让出现频率高的字符位于的深度尽量小。
算法过程：
频率表：A：60    B: 45   D: 20 E:3 F: 5
1、从小到大排序：E F D B A
2、

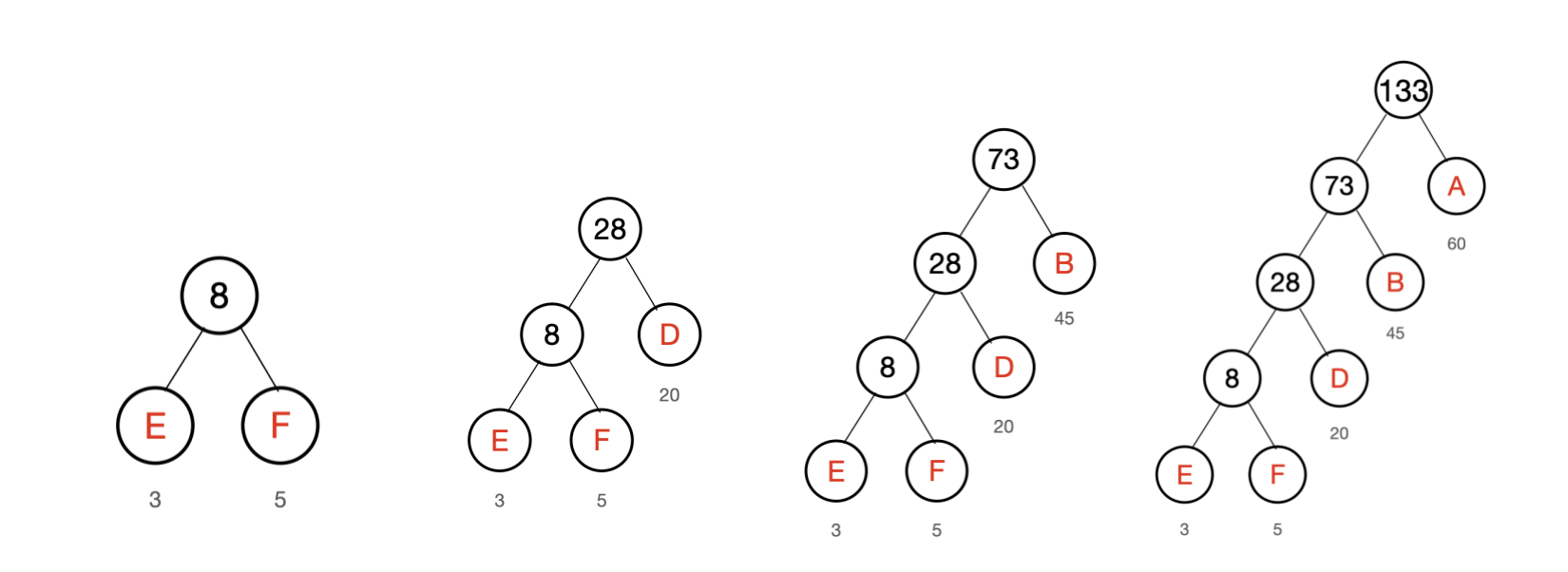
通过上述方法构造出来的树即哈夫曼树。

3、设计

#include<bits/stdc++.h>
using namespace std;

typedef struct
{
    int weight;
    char ch;
    int parent;
    int leftchild;
    int rightchild;	
}Huffman;

typedef struct Hcode
{
    int code[100]; 
    int start;           
};

Huffman huffman[100];
Hcode code[100];

void HuffmanTree(int n)
{
	int a,b,c,d;
    for (int i=0;i<n*2-1;++i)
	{
        huffman[i].weight=0;
        huffman[i].parent=-1;
        huffman[i].leftchild=-1;
        huffman[i].rightchild=-1;
    }
    for (int i=0;i<n;i++)
	{
        cin >> huffman[i].ch;
        scanf("%d",&huffman[i].weight);
    }
    for (int i=0;i<n-1;i++)
	{
        a=b=-1;
        c=d=10000;
        for (int j=0;j<n+i;j++)
		{
            if (huffman[j].parent==-1 && huffman[j].weight<c)
			{
                d=c;
                b=a;
                a=j;
                c=huffman[j].weight;
            }
            else if (huffman[j].parent==-1 && huffman[j].weight<d)
			{
                b=j;
                d=huffman[j].weight;
            }
        }
        huffman[n+i].leftchild=a;
        huffman[n+i].rightchild=b;
        huffman[n+i].weight=c+d;
        huffman[a].parent=n+i;
        huffman[b].parent=n+i;
    }
}
void printHuffmanTree(int n)
{
    Hcode tcode;
    int curParent;
    int c;
    for (int i = 0; i < n; ++i){
        tcode.start = n - 1;
        c = i;
        curParent = huffman[i].parent;
        while (curParent != -1)
		{
            if (huffman[curParent].leftchild == c)
			{
                tcode.code[tcode.start] = 0;
            }
            else
			{
                tcode.code[tcode.start] = 1;
            }
            tcode.start--;
            c=curParent;
            curParent=huffman[c].parent;
        }
        for(int j=tcode.start+1;j<n;j++)
		{
            code[i].code[j] = tcode.code[j];
        }
        code[i].start = tcode.start;
    }
}
int main()
{
	int n=0;
    scanf("%d",&n);
    HuffmanTree(n);
    printHuffmanTree(n);
    for (int i=0;i<n;++i)
	{
        printf("%c :",huffman[i].ch);
        for (int j=code[i].start+1;j<n;++j)
		{
            printf("%d",code[i].code[j]);
        }
        printf("\n");
    }
    return 0;
}

4、分析

排序： \(O(nlogn)\) ，对于树的遍历： \(O(nlogn)\) ，总时间复杂度： \(O(nlogn)\) 。

5、源码

https://github.com/HaHe-a/Algorithm-analysis-and-design-code/blob/master/huffman.cpp