算法分析与设计(work2)

问题

给出一幅有n个顶点，m条边构成的图，求解各个顶点之间的最短距离。

解析

Floyd 算法：
Floyd 算法的本质是动态规划。我们考虑两个点之间的最短路径只有两种可能，
第一种：起点直接通过一条路径到达终点。第二种：从一个点出发经过若干个别的点，然后到达终点。
那么我们就可以通过枚举中间点k，去判断是否存在比原来路径更短的路径，即如果 \(dis(i,k)+dis(k,j)<dis(i,j)\)，那么 \(dis(i,j)\) 就可以更新为 \(dis(i,k)+dis(k,j)\)。遍历完所有节点k，就出来的 \(dis(i,j)\) 就是i->j的最短路径。
作业中给出的图的距离矩阵：

经过Floyd算法处理后得到的距离矩阵为：

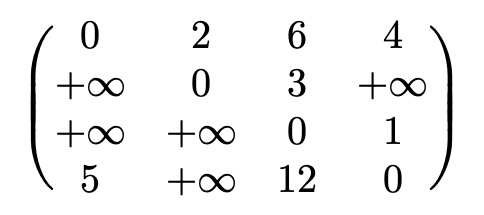
由此就可以得到各顶点之间的最短距离。

Dijkstra算法：
Dijkstra算法是使用贪心算法实现的。首先把起点把所有点的距离存下来找最短的，然后松弛一次再找最短的，松弛操作就是遍历一遍把刚才找到的点作为中转点其它点的距离会不会更近。最后就可以找到最短的路径。

设计

Floyd算法伪代码：

for(k=one of all vertex)
    for(i=one of all vertxt)
        for(j=one if all vertex)
            if(distance(i,k)+distance(k,j)<distance(i,j)) update distance(i,j)

Dijkstra算法伪代码：

Init ,  pre-populate PQ
while !PQ.empty() // PQ is a Priority Queue
  for each neighbor v of u = PQ.front(), PQ.pop()
        relax(u, v, w(u, v)) + update PQ

分析

Floyd算法：
在Floyd算法中，首先需要遍历n个点，然后对于每对点的遍历需要 \(O(n^2)\)的复杂度，这些遍历是在枚举中间的循环内的，时间复杂度\(O(n)\times O(n^2)=O(n^3)\)。
Dijkstra算法：
朴素算法：当对于某个点，需要遍历和这条边相连的每一条边找出最小值，那么时间复杂度 \(O(n^2)\)。很容易想到用堆优化每次去最小值，那么时间复杂度为 \(O(nlogn)\)。

源码

https://github.com/HaHe-a/Algorithm-analysis-and-design-code/tree/master/Desktop/work2