算法分析与设计(work1)

问题：

给出由 \(n\) 个点， \(m\) 条边构成的一幅无向图，分别用Prim算法和Kruskal算法构造一棵最小生成树。

解析：

Prim算法：

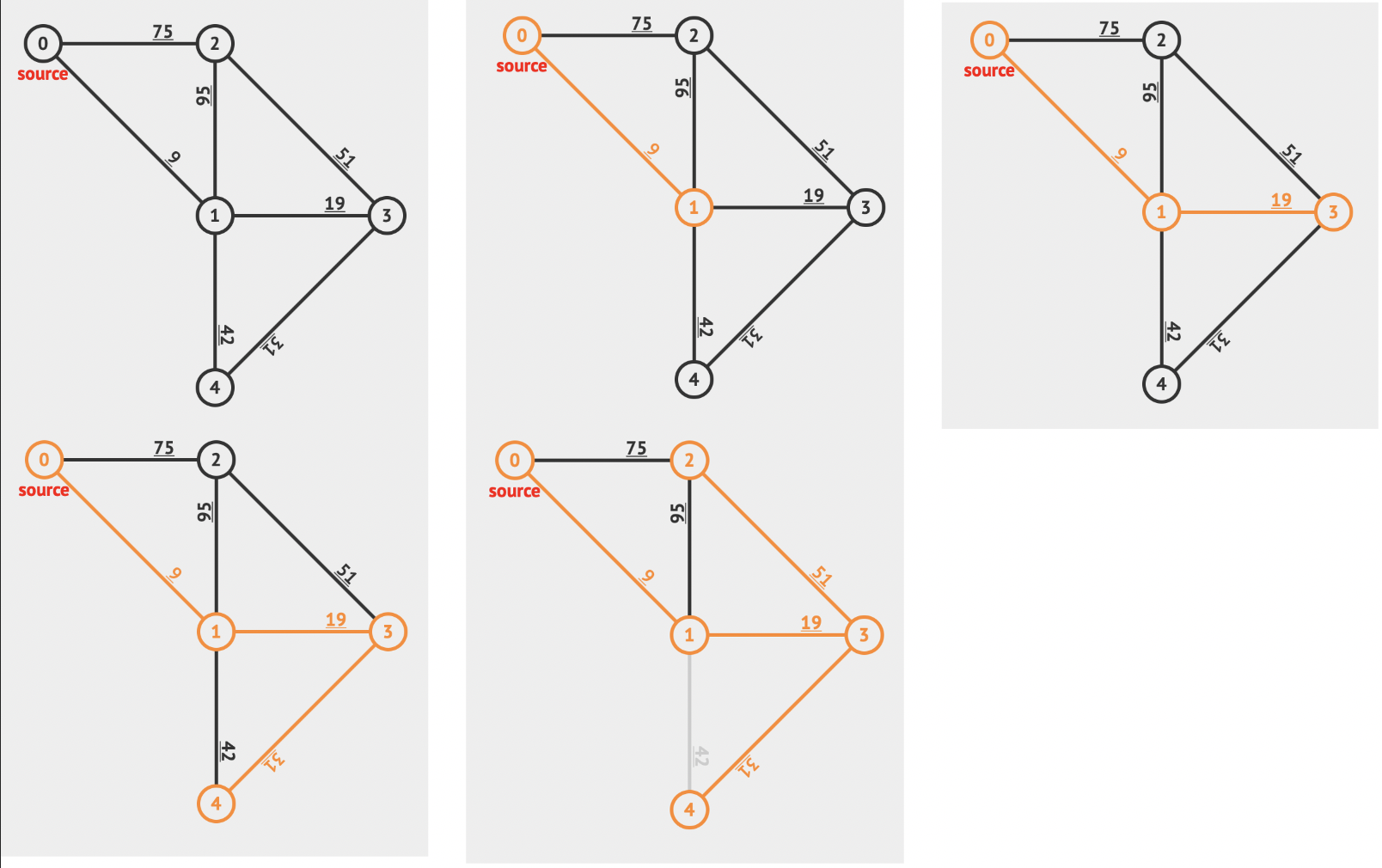
从任意一个顶点开始生成最小生成树，每次选择和当前已经构成的树的最小边，把最小边连接的顶点加入到树中，直到所有顶点都被加入。
图示：

Kruskal算法：

先对所有边按升序进行排序，然后从小到大遍历所有边，如果这条边连接的两个点不联通，则加入这条边，直到用n-1条边构成一棵树。在判断点是否连通可以用并查集维护。
图示：

设计：

伪代码：

Prim算法：

T = {s}
enqueue edges connected to s in PQ (by inc weight)
while (!PQ.isEmpty){
    if (vertex v linked with e = PQ.remove ∉ T){
 	    T = T ∪ {v, e}, enqueue edges connected to v
    }else {
        ignore e
    }
}
MST = T 

Kruskal算法：

Sort E edges by increasing weight
T = {}
for (i = 0; i < edgeList.length; i++){
    if adding e = edgelist[i] does not form a cycle {
        add e to T
    }else{
        ignore e
    }
}
MST = T

分析：

Prim算法：

Prim算法在遍历 \(n\) 个点时，每次需要遍历和当前树没有连通的边，时间时间复杂度 \(O(n^2)\)。

Kruskal算法：

Kruskal算法首先需要排序，时间复杂度 \(O(nlogn)\) ，然后从小到大选边，其中用来判断是否连通的并查集算法，时间复杂度 \(O(logn)\) ，选取完 \(n-1\) 条边最坏情况时遍历 \(m\) 次，总时间复杂度 \(O(nlogn)\) 。

源码：

github地址：https://github.com/HaHe-a/Algorithm-analysis-and-design-code