tarjan求强连通分量 + 缩点 + 求割点割边

强连通分量：

       引用度娘：“有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。”

       就是在一幅图里，任意两点可以相互到达，这一幅图就是一个强连通分量。

       

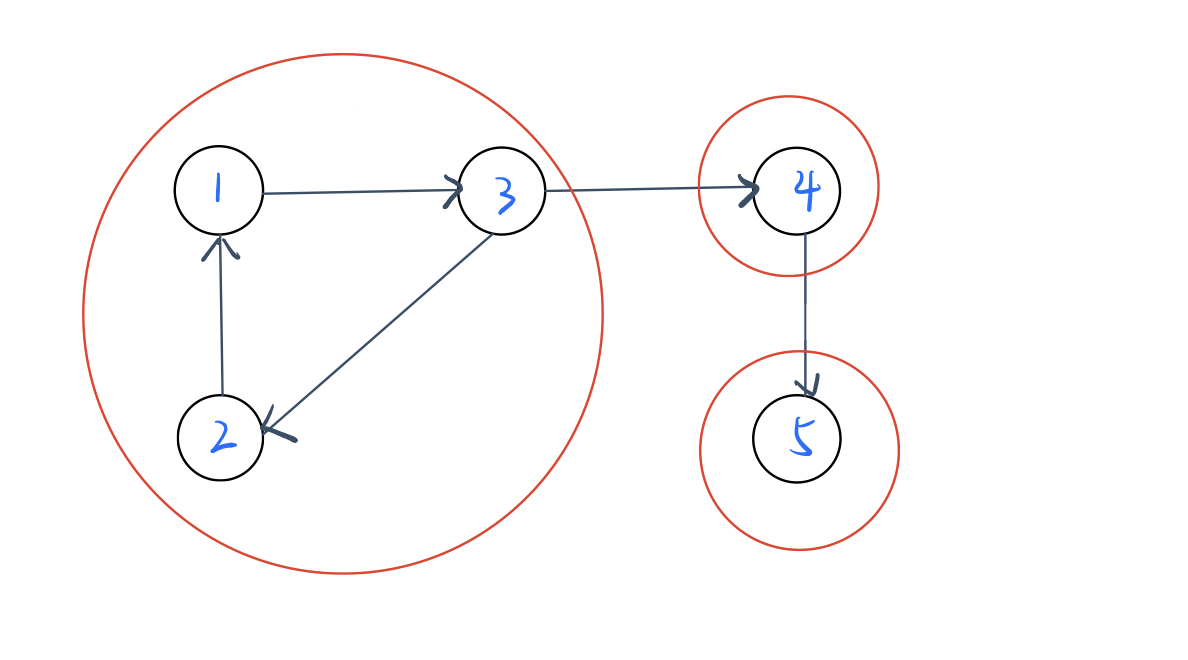
       这幅图中强连通分量有三个，为：1-2-3、4、5 。

强连通分量的应用：

       1、缩点。 

       2、求割点和割边的数量。

代码：

tarjan 模版 + 缩点

#include<bits/stdc++.h>
#define ll long long
#define MOD 998244353 
#define INF 0x3f3f3f3f
#define mem(a,x) memset(a,x,sizeof(a))  
using namespace std;
int dfn[50005];
int low[50005];
int vis[50005];
int stacks[50005];
int color[50005];
int cnt[50005];
int deep,sum,top;
int n,m;
vector<int>g[50005];
void tarjan(int u)
{
   dfn[u]=++deep;
   low[u]=deep;
   vis[u]=1;
   stacks[++top]=u;
   for(int i=0;i<g[u].size();i++){
       int v=g[u][i];
       if(!dfn[v])
       {
          tarjan(v);
          low[u]=min(low[u],low[v]);
       }else{
           if(vis[v]){
              low[u]=min(low[v],low[u]);
           }
       }
   }
   if(dfn[u]==low[u])
   {
      color[u]=++sum;
      vis[u]=0;
      while(stacks[top]!=u)
      {
          color[stacks[top]]=sum;
          vis[stacks[top--]]=0;
      }
      top--;
   }
}
int main()
{
    deep=0;
    top=0;
    sum=0;
    mem(dfn,0);
    mem(vis,0);
    mem(cnt,0);
    scanf("%d %d",&n,&m);
    while(m--){
       int from,to;
       scanf("%d %d",&from,&to);
       g[from].push_back(to);
    }
    for(int i=1;i<=n;i++){
        if(!dfn[i]){
           tarjan(i);
        }
    }
    int num=0;
    for(int i=1;i<=n;i++){
        cnt[color[i]]++;
    }
    for(int i=1;i<=sum;i++){
      if(cnt[i]>1)num++;
    }
    cout<<num;
    return 0;
}

 

tarjan 求割点

在原来的tarjan 基础上 加一个特判：如果一个点的为根节点且这个点有两个及以上的儿子，这个点就是割点。

代码：

#include<bits/stdc++.h>
#define ll long long
#define MOD 998244353 
#define INF 0x3f3f3f3f
#define mem(a,x) memset(a,x,sizeof(a))  
using namespace std;
int n,m;
int deep=0,root;
vector<int>g[200015];
int dfn[100015];
int low[100015];
int stack[100015];
int vis[100015];
int iscut[100015];
int tarjan(int u,int fa)
{
    int child=0,lowu;
    lowu=dfn[u]=++deep;
    int sz=g[u].size();
    for(int i=0;i<sz;i++)
    {
        int v=g[u][i];
        if(!dfn[v])
        {
            int v=g[u][i];
            int lowv=tarjan(v,u);
            lowu=min(lowu,lowv);
            if(lowv>dfn[u])
            {
                iscut[u]=1;
            }
        }else{
            if(v!=fa&&dfn[v]<dfn[u])
            {
                lowu=min(lowu,dfn[v]);
            }
        }
    }
    if(fa<0&&child==1)
    {
        iscut[u]=0;
    }
    low[u]=lowu;
    return lowu;
}
int main()
{
     scanf("%d %d",&n,&m);
     for(int i=1;i<=m;i++){
         int from,to;
         scanf("%d %d",&from,&to);
         g[from].push_back(to);
         g[to].push_back(from);
     }
     for(int i=1;i<=n;i++){
         if(!vis[i]){
           root=i;
           tarjan(i,-1);
         }
     }
     int ans=0;
     for(int i=1;i<=n;i++){
         if(iscut[i]){
             ans++;
         }
     }
     printf("%d\n",ans);
     for(int i=1;i<=n;i++){
         if(iscut[i]){
             printf("%d ",i);
         }
     }
     return 0;
}

求割边

#include<cstdio> 
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define hi printf("hi!");
using namespace std;

vector<pair<int,int> >bridge;
vector<int> g[10010];
int dfn[10010],low[10010];
int deep,root,n,m,ans;

int tarjan(int u,int fa)
{
    int lowu;
    lowu=dfn[u]=++deep;
    int sz=g[u].size();
    for(int i=0;i<sz;i++)
    {
        int v=g[u][i];
        if(!dfn[v])
        {
            int lowv=tarjan(v,u);
            lowu=min(lowu,lowv);
            if(lowv>dfn[u])
            {
                int from,to;
                from=u;
                to=v;
                if(from>to)
                {
                    swap(from,to);
                }
                bridge.push_back(make_pair(from,to));
            }
        }
        else
        {
            if(v!=fa&&dfn[v]<dfn[u])
            {
                lowu=min(lowu,dfn[v]);
            }
        } 
    }
    low[u]=lowu;
    return lowu;
} 

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int from,to;
        scanf("%d%d",&from,&to);
        g[from].push_back(to);
        g[to].push_back(from);
    }
    for(int i=1;i<=n;i++)
    {
        if(!dfn[i])
        {
            root=i;
            tarjan(i,-1);
        }
    }
    for(int i=0;i<bridge.size();i++)
    {
        printf("%d %d\n",bridge[i].first,bridge[i].second);
    }
}