Codeforces Round #662 (Div. 2)（A B C D）

 

A. Rainbow Dash, Fluttershy and Chess Coloring

题意：给你一个 n*n的矩阵，让你在其中涂上蓝红两种颜色，每一次可以涂色的格子为旁边没有与当前要涂的颜色的相反颜色的格子，即不可能出现相同颜色的相邻格子。

思路：每次贪心，涂尽量多的格子，在找规律。即如图所示，答案就是 n/2+1。

                                                   

代码：

 1 #include<bits/stdc++.h>
 2 #define ll long long
 3 #define MOD 998244353 
 4 #define INF 0x3f3f3f3f
 5 #define mem(a,x) memset(a,x,sizeof(a))  
 6 #define _for(i,a,b) for(int i=a; i< b; i++)
 7 #define _rep(i,a,b) for(int i=a; i<=b; i++)
 8 #define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
 9 using namespace std;
10     
11 int main()
12 {   
13     int t;
14     scanf("%d",&t);
15     while(t--){
16        int n;
17        cin>>n;
18        cout<<n/2+1<<endl;
19     }
20     return 0;        
21 }
View Code

 

B. Applejack and Storages

题意：给你 n 条边，再给你 q 次操作，问你在每次操作后，这些边是否能组成一个正方形和一个矩形。

思路：用 num[ ]数组维护拥有各长度边的总数，用四个变量维护总数大于等于8、大于等于6、大于等于4、大于等于2的各长度边的数量，最后通过对这些变量的判断来确定。

代码：

  1 #include<bits/stdc++.h>
  2 #define ll long long
  3 #define MOD 998244353 
  4 #define INF 0x3f3f3f3f
  5 #define mem(a,x) memset(a,x,sizeof(a))  
  6 #define _for(i,a,b) for(int i=a; i< b; i++)
  7 #define _rep(i,a,b) for(int i=a; i<=b; i++)
  8 #define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  9 using namespace std;
 10  
 11 int a[100005];
 12 bool cmp(int x,int y)
 13 {
 14   return x>y;
 15 }    
 16 int main()
 17 {   
 18   int n,q;
 19   int a6=0,b4=0,c2=0,a8=0;
 20   mem(a,0);
 21   scanf("%d",&n);
 22   for(int i=1;i<=n;i++){
 23      int x;
 24      scanf("%d",&x);
 25      a[x]++;
 26   }
 27   for(int i=1;i<=100000;i++){
 28      if(a[i]>=8){
 29        a8++;
 30      }
 31      if(a[i]>=6&&a[i]<8){
 32        a6++;
 33      }
 34      if(a[i]>=4&&a[i]<6){
 35        b4++;
 36      }
 37      if(a[i]>=2&&a[i]<4){
 38        c2++;
 39      }
 40   }
 41   scanf("%d",&q);
 42       
 43   while(q--){
 44      getchar();
 45      char c;
 46      int x;
 47      scanf("%c %d",&c,&x);
 48      if(c=='+'){
 49         a[x]++;
 50         if(a[x]==2){
 51           c2++;
 52         }
 53         if(a[x]==4){
 54            c2--;
 55            b4++;
 56         }
 57         if(a[x]==6){
 58            a6++;
 59            b4--;
 60         }
 61         if(a[x]==8){
 62            a8++;
 63            a6--;
 64         }
 65      }else if(c=='-'){
 66         a[x]--;
 67         if(a[x]==1){
 68            c2--;
 69         }
 70         if(a[x]==3){
 71            b4--;
 72            c2++;
 73         }
 74         if(a[x]==5){
 75            a6--;
 76            b4++;
 77         }
 78         if(a[x]==7){
 79            a8--;
 80            a6++;
 81         }
 82      }
 83      if(a8>=1){
 84         cout<<"YES"<<endl;
 85      }else{
 86      if(a6>=1){
 87         if(b4>=1||c2>=1||a6>=2){
 88            cout<<"YES"<<endl;
 89         }else{
 90              cout<<"NO"<<endl;
 91         }
 92      }else{
 93         if(b4>=1){
 94            if((b4>=2)||(c2>=2)){
 95               cout<<"YES"<<endl;
 96            }else{
 97               cout<<"NO"<<endl;
 98            }
 99         }else{
100            cout<<"NO"<<endl;
101         }
102      }
103   }
104   }
105   return 0;        
106 }
View Code

 

C. Pinkie Pie Eats Patty-cakes

题意：给你 n 个食物，每个数字代表食物编号，问你怎样排序可以使所有吃到相同食物的间隔的最小值最大。

思路：找到数量最多的食物和最大数量的食物的总数，将这些取出来，按如图的顺序进行排序组成隔板。

     在隔板间添加其他数字即可使最小值最大。

代码：

#include<bits/stdc++.h>
#define ll long long
#define MOD 998244353 
#define INF 0x3f3f3f3f
#define mem(a,x) memset(a,x,sizeof(a))  
#define _for(i,a,b) for(int i=a; i< b; i++)
#define _rep(i,a,b) for(int i=a; i<=b; i++)
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
 
int a[100005];
int num[100005];
int main()
{   
  int t,n;
  scanf("%d",&t);
  while(t--){
     scanf("%d",&n);
     mem(num,0);
     int maxn=0;
     for(int i=1;i<=n;i++){
      scanf("%d",&a[i]);
      num[a[i]]++;
      maxn=max(num[a[i]],maxn);
     }
     int x=0;
     for(int i=1;i<=n;i++){
       if(num[i]==maxn){
          x++;
       }
     }
     int p=n-maxn*x;
     cout<<x+p/(maxn-1)-1<<endl;
  }
  return 0;        
}
View Code

 

D. Rarity and New Dress

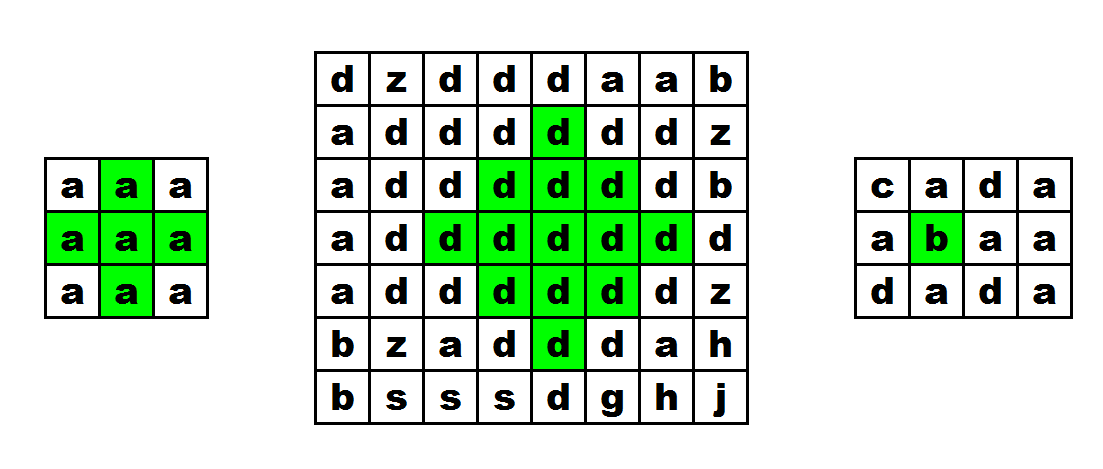
题意：给你n*m的矩形，每个放个有一个字母，问你在矩形中一共有多少个 斜正方形（如图所示的图形）。

思路：dp题，dp[ i ][ j ] 表示 以第 i 行 第 j 列的方块为底部的 斜正方形的数量。也就是寻找这个点向上延申的斜正方形的数量。那么我们就要去确定这个点向上延申的方块数量是由哪几个点维护的。

先看图一，我们首先要判断点 （i-1,j)  （i-1,j-1)    (i-1,j+1)   (i-2.j)这四个点是否和底部点一致，如果不一致，那么这个底部点就只能构成 1 个斜正方形。否则，我们就要看[i-1][j-1]、[i-1][j+1]、[i-2][j]这三个点所可以构成的斜正方形的数量，看一下图二（只看绿色部分），以点[i-1][j-1]为底部可以构成 2 个斜正方形（包括自身），同理以另外两个点也是只有两个斜正方形，那么由[ i ][ j ]点维护的dp[ i ][ j ]=2+1=3，因为有三个点同时维护，因此需要这三个的最小值，因此dp转移方程为 dp[ i ][ j ] = min(dp[ i-1 ][ j-1 ]，dp[ i-1 ][ j+1 ]，dp[ i-2][ j ])+1  。

 

代码：

 1 #include<bits/stdc++.h>
 2 #define ll long long
 3 #define MOD 998244353 
 4 #define INF 0x3f3f3f3f
 5 #define mem(a,x) memset(a,x,sizeof(a))  
 6 #define _for(i,a,b) for(int i=a; i< b; i++)
 7 #define _rep(i,a,b) for(int i=a; i<=b; i++)
 8 #define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
 9 using namespace std;
10  
11 char mp[2005][2005];
12 int dp[2005][2005];
13 int main()
14 {   
15   int n,m;
16   ll sum=0;
17   scanf("%d %d",&n,&m);
18   for(int i=1;i<=n;i++){
19     getchar();
20     for(int j=1;j<=m;j++){
21         scanf("%c",&mp[i][j]);
22     }
23   }
24   for(int i=1;i<=n;i++){
25      for(int j=1;j<=m;j++){
26           dp[i][j]=1;
27           if(i>=3&&j>=2&&mp[i][j]==mp[i-2][j]&&mp[i][j]==mp[i-1][j-1]&&mp[i][j]==mp[i-1][j+1]&&mp[i][j]==mp[i-1][j]){
28              dp[i][j]=min(dp[i-2][j],min(dp[i-1][j-1],dp[i-1][j+1]))+1;
29           }
30           sum+=(ll)dp[i][j];
31      }
32   }
33   cout<<sum<<endl;
34   return 0;        
35 }
View Code

 

posted @ 2020-08-08 18:42  hachuochuo  阅读(132)  评论(0)  编辑  收藏  举报