17373194陈丛文第一次项目作业

课程：北航-2020-春-软件工程	博客园班级博客
项目	内容
要求：求交点个数	个人项目作业
班级：005	Sample
GitHub地址	IntersectProject

一、PSP估算

在开始实现程序之前，在下述 PSP 表格记录下你估计将在程序的各个模块的开发上耗费的时间。（0.5'）
在你实现完程序之后，在下述 PSP 表格记录下你在程序的各个模块上实际花费的时间。（0.5'）

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	10	10
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	60	120
· Design Spec	· 生成设计文档	10	10
· Design Review	· 设计复审 (和同事审核设计文档)	0	0
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	20	0
· Design	· 具体设计	20	20
· Coding	· 具体编码	60	120
· Code Review	· 代码复审	20	30
· Test	· 测试（自我测试，修改代码，提交修改）	60	60
Reporting	报告
· Test Report	· 测试报告	30	30
· Size Measurement	· 计算工作量	20	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	60	60
	合计	370	470

可见自己对工作量的估算与实际情况相差较大，原因主要在于新技术的学习上。由于过去使用c++的频率比较低，因此这次项目正式开工前把大量的时间花在了学习c++上.

二、思路及设计

解题思路描述。即刚开始拿到题目后，如何思考，如何找资料的过程。（3'）

设计实现过程。设计包括代码如何组织，比如会有几个类，几个函数，他们之间关系如何，关键函数是否需要画出流程图？单元测试是怎么设计的？（4'）

代码说明。展示出项目关键代码，并解释思路与注释说明。（3'）

解题思路

经过思考这道题似乎并没有更好的办法，唯一的办法就是算出所有的交点并且去重。由于已经算过的图形没必要再算一遍，算法复杂度为O(n(n-1))=O(n^2).

对直线的表示使用y=kx+b的表示方法，基于2点考虑。第一这样写表示方法唯一，同时方便与圆计算求交点。第二这样写能够方便对于平行线的判定。但需要考虑一种特殊的直线x=t,对这样的直线采取特殊情况处理

所有交点共分为3种情况，共包括直线与直线的交点，直线与圆的交点以及圆与圆的交点，对每种情况采取单独的函数进行计算处理。

设计实现过程

首先设计Shape类作为所有图形的基类，之后设计Line类和Circle类，以及Point类.直线使用y=kx+b表示，圆使用(x-a)^2+（y-b)2=r^2表示，具体实现如下所示

class Shape {
public:string mtype;
      Shape(string i_type) {
          mtype = i_type;
      }
};
class Line :public Shape {
public:double ma, mb;
      int mspecial;//常规直线mspecial=0,垂直于X轴的直线mspecial=1,ma为X轴对应值
      Line() :Shape("L") {
          ma = 0;
          mb = 0;
          mspecial = 0;
      }
      Line(double input1, double input2, int ifspecial) :Shape("L") {
          ma = input1;
          mb = input2;
          mspecial = ifspecial;

      }
};
class Circle :public Shape {
public:double mx, my, mr;
      Circle() :Shape("C") {
          mx = 0;
          my = 0;
          mr = 0;
      }
      Circle(double input1, double input2, double input3) :Shape("C") {
          mx = input1;
          my = input2;
          mr = input3;

      }
}
class Point {
public:double x, y;
      Point(double input1, double input2) {
          x = input1;
          y = input2;
      }

};

需要注意的是对于point类,由于x,y都是double类型。在hash判断时有很小的概率会发生错误，但不能忽略，因此重写了它的Hash函数以及equal函数，如下所示。

struct Hash_Point {
    size_t operator()(const class Point& input1)const {
        //return (int)(((int)input1.x) * 1e6 / 10 + ((int)input1.y) * 1e6 / 10);
        long temp1 = (long)input1.x;
        long temp2 = (long)input1.y;
        return (temp1 + temp2) * 13 + (temp1 * 1000 % 1000 + temp2 * 1000 % 1000);
    }
};

struct Equal_Point {
    bool operator()(const class Point& input1, const class Point& input2)const {
        return abs(input1.x - input2.x) <= EPS && abs(input1.y - input2.y) <= EPS;
        //return input1.x == input2.x && input1.y == input2.y;
    }
};

采用了EPS规避计算导致double产生的较小误差，实际运行效率也还是不错的。

关于单元测试

单元测试分为3类，第一类是对于部分函数的测试，包括圆与直线是否存在交点，以及圆与圆之间是否存在焦点的判断。

第二类包括各种特殊情况，包括圆与圆外切，圆与圆内切以及直线与圆外切，直线与直线平行，多条线交于同一点，多个圆交于同一点的情况。

第三类使用随机产生的圆和直线进行测试，观察是否满足时间要求。

性能分析

第一次测试时如下图所示，delete函数占据了非常大的运算部分。猜测可能是参数传递时导致重复拷贝复制并删除造成，因此在接下来对其进行优化。

下图为优化后的结果，将所有实例传递全部改为指针传递,可见new代替了delete，但是所占比例大幅下降。

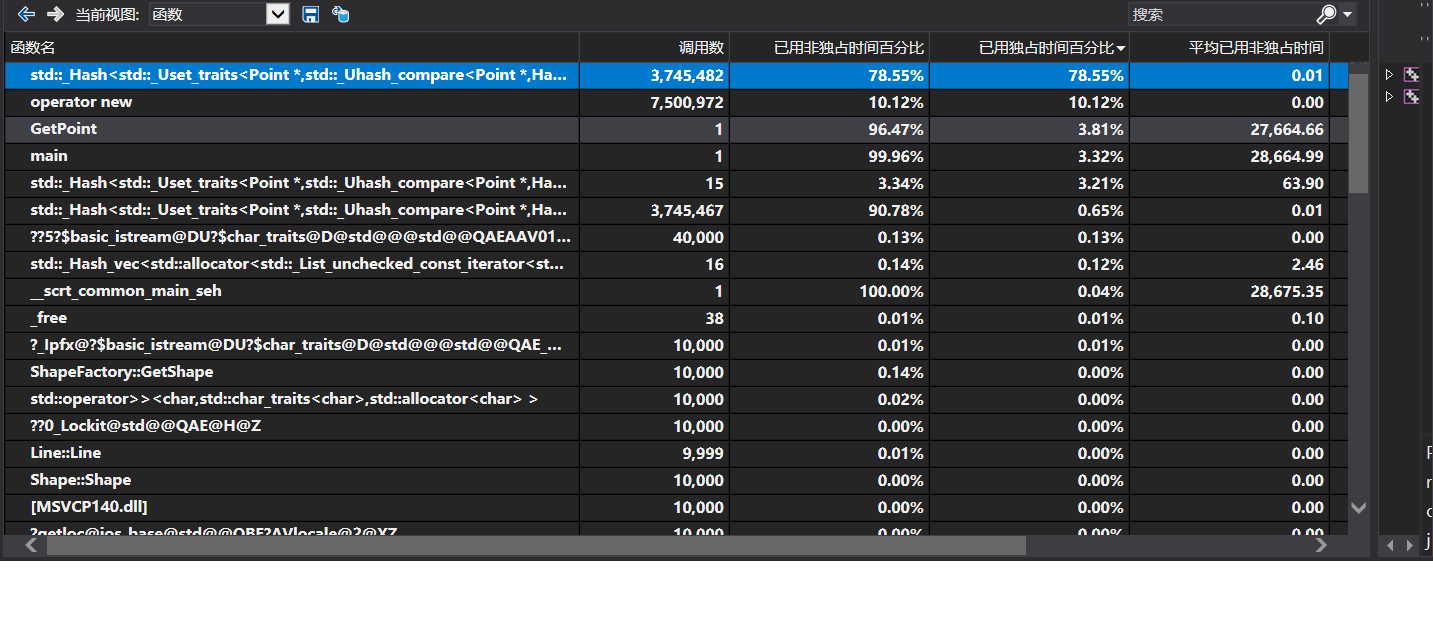
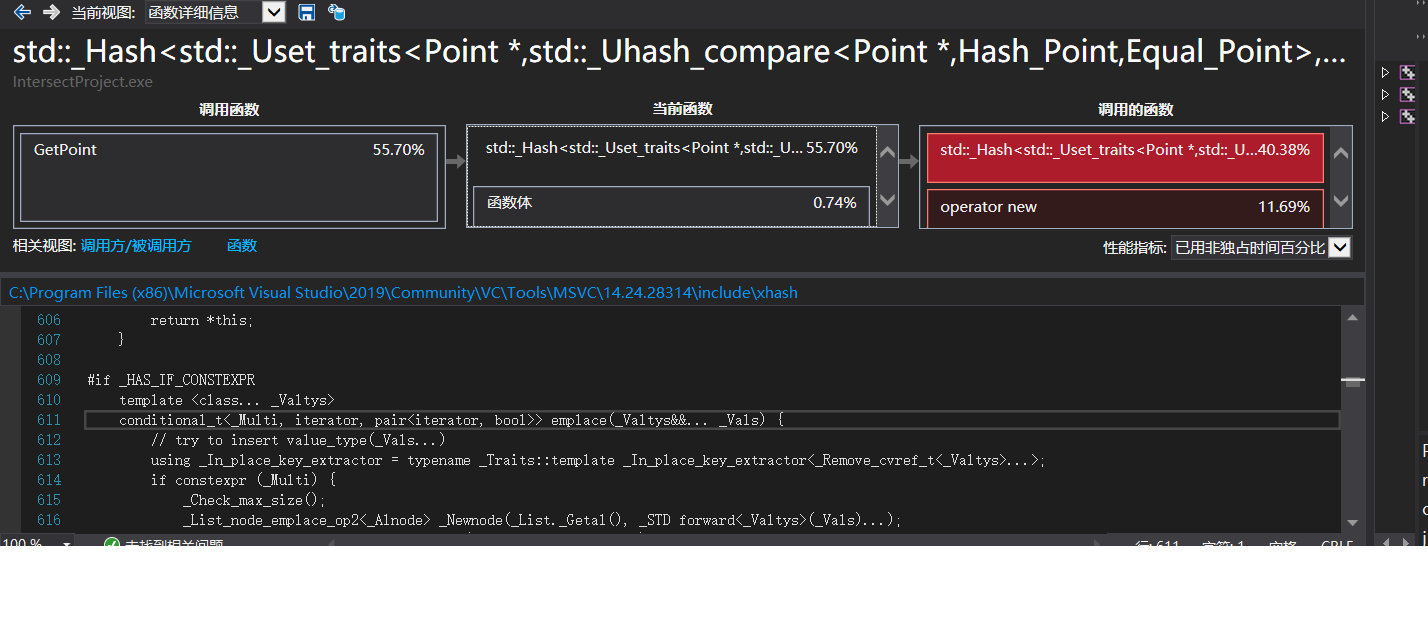
由于所有节点集使用unordered_set进行储存，因此hash函数使用了非常高频次。我对hash函数进行了优化，使得hash所需时间有一定幅度的减少.

代码说明

最为关键的代码是求交点部分的代码，具体如下所示。在具体代码计算之前先对直线是否平行进行判断，以及圆与直线距离是否大于圆的半径以及圆与圆是否互相包含或者圆与圆是否不相交，之后在计算具体交点时需要判断被除数为0的情况，具体代码如下所示:

void L2L(Line* input1, Line* input2, unordered_set<Point, Hash_Point, Equal_Point>& g_allpoint) {
    if (input1->mspecial == 0 && input2->mspecial == 0) {
        if (abs(input1->ma - input2->ma) <= EPS) {
            return;
        }
        double x = (input2->mb - input1->mb) / (input1->ma - input2->ma);
        double y = x * input1->ma + input1->mb;
        g_allpoint.insert(Point(x, y));
        return;
    }
    else if (input1->mspecial == 1 && input2->mspecial == 1) return;
    else {
        if (input1->mspecial == 1) {
            g_allpoint.insert(Point(input1->ma, input1->ma * input2->ma + input2->mb));
        }
        else {
            g_allpoint.insert(Point(input2->ma, input1->ma * input2->ma + input1->mb));
        }
    }
}
void C2C(Circle* input1, Circle* input2, unordered_set<Point, Hash_Point, Equal_Point>& g_allpoint) {
    double r2 = input2->mr, r1 = input1->mr, a1 = input1->mx, a2 = input2->mx, b1 = input1->my, b2 = input2->my;
    double x1 = 0, y1 = 0, x2 = 0, y2 = 0;
    if (abs(a1 - a2) < EPS && abs(b1 - b2) < EPS) return;
    else if (!Circle::C2DisJudge(input1, input2)) return;
    else if (abs(b1 - b2) < EPS) {
        x1 = (r2 * r2 - r1 * r1 + a1 * a1 - a2 * a2) / (2 * a1 - 2 * a2);
        y1 = sqrt(r1 * r1 - (x1 - a1) * (x1 - a1)) + b1;
        y2 = -sqrt(r1 * r1 - (x1 - a1) * (x1 - a1)) + b1;
        g_allpoint.insert(Point(x1, y1));
        g_allpoint.insert(Point(x1, y2));
        return;
    }
    else {
        double tempm = (r2 * r2 - r1 * r1 + a1 * a1 - a2 * a2 + b1 * b1 - b2 * b2) / (2 * b1 - 2 * b2);
        double tempk = -(2 * a1 - 2 * a2) / (2 * b1 - 2 * b2);
        double temp1 = (1 + tempk * tempk);
        double temp2 = 2 * tempk * (tempm - b1) - 2 * a1;
        double temp3 = a1 * a1 + (tempm - b1) * (tempm - b1) - r1 * r1;
        x1 = (-temp2 + sqrt(temp2 * temp2 - 4 * temp1 * temp3)) / (2 * temp1);
        x2 = (-temp2 - sqrt(temp2 * temp2 - 4 * temp1 * temp3)) / (2 * temp1);
        y1 = tempk * x1 + tempm;
        y2 = tempk * x2 + tempm;
        g_allpoint.insert(Point(x1, y1));
        g_allpoint.insert(Point(x2, y2));
    }
    return;
}
void C2L(Circle* input1, Line* input2, unordered_set<Point, Hash_Point, Equal_Point>& g_allpoint) {
    if (!Circle::CLDisJudge(input1, input2)) return;
    double x1 = 0, x2 = 0, y1 = 0, y2 = 0;
    double  r1 = input1->mr, a1 = input1->mx, b1 = input1->my;
    if (input2->mspecial == 1) {
        x1 = input2->ma;
        y1 = sqrt(r1 * r1 - (x1 - a1) * (x1 - a1)) + b1;
        y2 = -sqrt(r1 * r1 - (x1 - a1) * (x1 - a1)) + b1;
        g_allpoint.insert(Point(x1, y1));
        g_allpoint.insert(Point(x1, y2));
        return;
    }
    else {
        double tempm = input2->mb;
        double tempk = input2->ma;
        double temp1 = (1 + tempk * tempk);
        double temp2 = 2 * tempk * (tempm - b1) - 2 * a1;
        double temp3 = a1 * a1 + (tempm - b1) * (tempm - b1) - r1 * r1;
        x1 = (-temp2 + sqrt(temp2 * temp2 - 4 * temp1 * temp3)) / (2 * temp1);
        x2 = (-temp2 - sqrt(temp2 * temp2 - 4 * temp1 * temp3)) / (2 * temp1);
        y1 = tempk * x1 + tempm;
        y2 = tempk * x2 + tempm;
        g_allpoint.insert(Point(x1, y1));
        g_allpoint.insert(Point(x2, y2));
    }
}

这部分大量计算可能产生一定的误差，但大概率不会超过EPS规定的误差范围。

Code Quality Analysis

需要处理的问题大多在于_s函数的使用。由于visual studio似乎对编程安全性要求较高，因此大量函数必须采用__s安全形式。

posted @ 2020-03-10 10:50 h87d 阅读(200) 评论(2) 编辑收藏举报

刷新页面返回顶部

h87d

17373194陈丛文第一次项目作业