浅谈匈牙利算法
二分图最大匹配的模板。
对于二分图:
我们称,一个图中,当且仅当其没有奇环时,是一个二分图。
那么,最大二分图匹配就是:
给定二分图,现在要选出一些边,使得与每一个点相连的边最多选出一条,求最多选出的边数。
当所有边都被匹配上时,称之为一个完美的二分图匹配。
来一个例题吧:
从前有a个男生和b个女生,有一些男女之间有互相喜欢的关系,现在它们想要两两配对,怎样配对才能让配成的对数尽可能多?
这就是上面那一句话啊。
我们来模拟一下匈牙利算法的流程。
我们规定:第一天,每个男生按顺序取找女生表白。
其中,每个女生每天只能被表白一次。
对于找到的女生,如果她没有对象,就暂时接受。
如果有,就让她原来的对象尝试去找新的女生表白。
如果他成功的,她就抛弃他,去接受这个新的。
否则,就拒绝这个新来的。
例如:
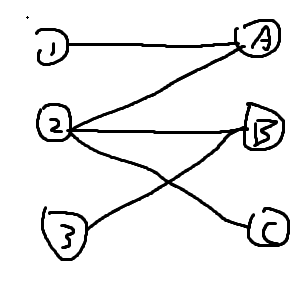
1,2.3是男生,ABC是女生。
引入老师的话:
第一天,1向A表白,A答应了。
第二天,2向A表白,A说“可是我已经答应1了耶,要不你去跟他商量商量?”于是2来到1的家里,谁知1拔出手枪指向2喊“滚!”
第三天,2向B表白,B答应了。
第四天,3向B表白,开着坦克隆隆地推到2家门口……
第五天,2向C表白……
匈牙利真是一个好地方!
就这样,这就是匈牙利(神奇的地方)算法!
于是,我们可以这样实现:
用临接表存边,暴力枚举A图中的点,再暴力枚举B图中的点。
令vis数组表示x点是否已经访问过,match表示x所匹配的点。
若已经访问过,pass.
没有的话,判断:
当它没有匹配或者是它匹配的点换人了,它就要尝试去换了。
这时返回true。
如果一直没有匹配到,就返回false好了。
把每次的结果加起来,求出A图中所有点的匹配数,即为答案。
代码:
#include<cstdio> #include<iostream> #include<cstring> using namespace std; int match[500000],vis[500000]; int n,m,E,ans,head[500000],tot; struct node{ int nxt,to; }e[500000]; inline void add(int x,int y){ e[++tot].nxt=head[x]; e[tot].to=y; head[x]=tot; } void read(int &x) { x=0; int f=1; char ch=getchar(); while (ch<'0'||ch>'9') { if (ch=='-')f=-f; ch=getchar(); }while (ch>='0'&&ch<='9') { x=x*10+ch-48; ch=getchar(); }x*=f; } bool dfs(int x){ for(int i=head[x];i;i=e[i].nxt){ int j=e[i].to; if(vis[j])continue; vis[j]=1; if(!match[j]||dfs(match[j])){ match[j]=x; return true; } }return false; } void work(){ for(int i=1;i<=n;++i){ memset(vis,0,sizeof(vis)); ans+=dfs(i); } } int main(){ read(n);read(m);read(E); for(int i=1;i<=E;++i){ int x,y; read(x);read(y); if(x>=1&&x<=n&&y>=1&&y<=m){add(x,y);} } work(); printf("%d\n",ans); return 0; }

