题解【大融合】

刚刚学了学LCT维护子树信息，FlshHu大佬太强了%%%

题目描述

小强要在NN个孤立的星球上建立起一套通信系统。这套通信系统就是连接NN个点的一个树。 这个树的边是一条一条添加上去的。在某个时刻，一条边的负载就是它所在的当前能够 联通的树上路过它的简单路径的数量。

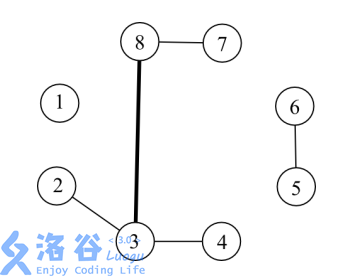
例如，在上图中，现在一共有了55条边。其中，(3,8)(3,8)这条边的负载是66，因 为有六条简单路径2-3-82−3−8,2-3-8-72−3−8−7,3-8,3-8-73−8,3−8−7,4-3-84−3−8,4-3-8-74−3−8−7路过了(3,8)(3,8)。

现在，你的任务就是随着边的添加，动态的回答小强对于某些边的负载的 询问。

输入输出格式

输入格式：

 

第一行包含两个整数 N, QN,Q,表示星球的数量和操作的数量。星球从 11 开始编号。

接下来的 QQ 行，每行是如下两种格式之一：

• A x y 表示在 xx和 yy 之间连一条边。保证之前 xx 和 yy是不联通的。
• Q x y表示询问 (x,y)(x,y) 这条边上的负载。保证 xx 和 yy 之间有一条边。

 

输出格式：

 

对每个查询操作，输出被查询的边的负载。

解：

首先，来思考一下对于维护虚子树信息如何pushup.

实子树很简单，虚加实咯。

对于每一次access和link操作，应该更新修改一下当前的虚子树信息。因为这时它的父子关系发生的改变。

比如本题的pushup，就应该是左右实子树信息加上自己的虚子树信息+1.

也可以用来求子树和，改成sum即可。

推荐FlashHudalao的博客。

代码：

#include<cstdio>
#include<iostream>
using namespace std;
struct node{
    int s,si,fa,ch[2],val,rev;
}tr[500000];
char ch[4];
inline void pushup(int x){
    tr[x].s=tr[tr[x].ch[0]].s+tr[tr[x].ch[1]].s+tr[x].si+1;
}inline void pushr(int x){
    if(!x)return;
    swap(tr[x].ch[0],tr[x].ch[1]);
    tr[x].rev^=1;
}inline void pushdown(int x){
    if(tr[x].rev){
        pushr(tr[x].ch[0]);
        pushr(tr[x].ch[1]);
        tr[x].rev=0;
    }
}inline bool root(int x){
    int g=tr[x].fa;
    return !(tr[g].ch[0]==x||tr[g].ch[1]==x);
}inline void update(int x){
    if(!root(x))update(tr[x].fa);
    pushdown(x);
}inline void rotate(int x){
    int y=tr[x].fa,z=tr[y].fa,k=tr[y].ch[1]==x;
    if(!root(y))tr[z].ch[tr[z].ch[1]==y]=x;
    tr[x].fa=z;tr[y].ch[k]=tr[x].ch[k^1];
    if(tr[x].ch[k^1])tr[tr[x].ch[k^1]].fa=y;
    tr[x].ch[k^1]=y;tr[y].fa=x;pushup(y);pushup(x);
}inline void splay(int x){
    int y,z;
    update(x);
    while(!root(x)){
        y=tr[x].fa,z=tr[y].fa;
        if(!root(y))(tr[y].ch[1]==x)^(tr[z].ch[1]==y)?rotate(x):rotate(y);
        rotate(x);
    }pushup(x);
}inline void access(int x){
    for(int y=0;x;y=x,x=tr[x].fa){
        splay(x);
        tr[x].si+=tr[tr[x].ch[1]].s;
        tr[x].ch[1]=y;
        tr[x].si-=tr[tr[x].ch[1]].s;
        pushup(x);
    }
}inline void makeroot(int x){
    access(x);splay(x);pushr(x);
}inline void split(int x,int y){
    makeroot(x);access(y);splay(y);
}inline void link(int x,int y){
    split(x,y);tr[x].fa=y;
    tr[tr[x].fa].si+=tr[x].s;pushup(y);
}int n,q,a,b;
int main(){
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;++i)tr[i].s=1;
    for(int i=1;i<=q;++i){
        cin>>ch;
        if(ch[0]=='A'){
            scanf("%d%d",&a,&b);
            link(a,b);
        }else{
            scanf("%d%d",&a,&b);
            split(a,b);
            printf("%lld\n",(long long)(tr[a].si+1)*(tr[b].si+1));
        }
    }
    return 0;
}