Splay浅谈
Splay是众多平衡树之一,它的功能十分强大,但常数极大。在LCT和许多数据结构中都能用到。
Splay的核心操作,就是rotate。为了使树不是一条链,而是平衡的,我们需要旋转来维护形态。理论很简单,下面来看一下如何实现。
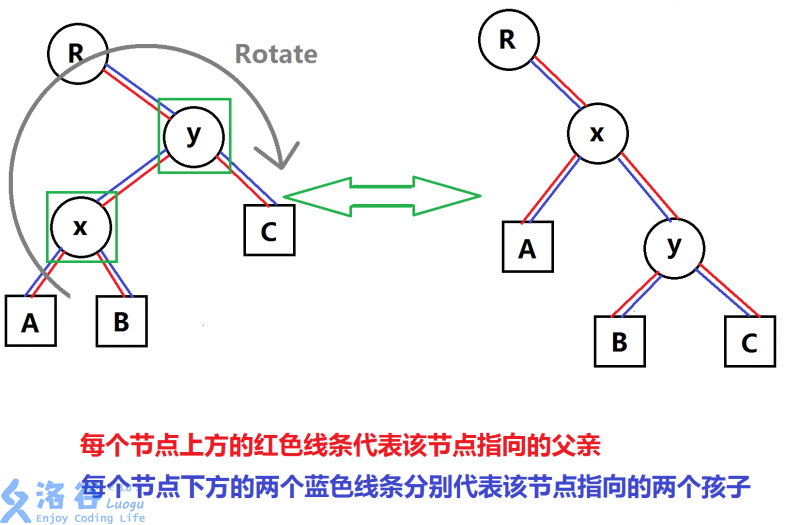
图片转自洛谷
我们注意到,旋转之后,这棵树依然保持着正常的大小关系。
来尝试着写代码。
观察到,y的c儿子依旧是y的右儿子,而x,y的父子关系发生了改变,x的左儿子不变,x的右儿子变成了y的左儿子。
这是右旋。
明显的,我们发现不只有这一种情况。单旋的Splay,会被出题人的构造数据卡成链。我们先来处理双旋操作,再来处理链。
Rotate:
inline void rotate(node *x){ node *y=x->fa,*z=y->fa;int k=y->ch[1]==x; z->ch[z->ch[1]==y]=x;x->fa=z; y->ch[k]=x->ch[k^1];x->ch[k^1]->fa=y; x->ch[k^1]=y;y->fa=x;pushup(y);pushup(x); }
注意,结构体里面存了x节点的父亲,左右儿子,值,子树大小以及此处值相同的节点个数。
其中,k=1表示y的右儿子是x,这是逻辑表达式。
理解了rotatw操作,开始讲一下它的核心:Splay操作。
还记得我说的单旋吗?在一些情况下,如果你只旋转当前节点,会依旧成为一条链。
我们如何避免这件事呢?
我们观察到,当x,x的fa以及grandfa在一条线上时,转x是无意义的。
所以,我们要rotate(y).
就这么简单。
这样一直到x转到目标点。
代码:
inline void splay(node *x,node *goal){ node *y,*z; while(x->fa!=goal){ y=x->fa,z=y->fa; if(z!=goal)(z->ch[1]==y)^(y->ch[1]==x)?rotate(x):rotate(y); rotate(x); }if(goal==null)rt=x; }
注意,此处我用的是指针,所以不是!goal,而是goal==null.
下面,就Splay模板开始讲解。
首先,插入操作。
我们插入一个点,首先判断,如果它是一棵空树,那就把树的根节点新建出来(指针),值为插入的值,return即可。
否则,往下沉。
有两种可能:在树中找的过程中,如果有值一样的,就把x旋转到根,并且把x的num++.
否则,新建节点,记录最后找到的点。
最后找到的点是新建点的father.
插入的值是新建点的值。
插入完成。
代码有些冗长,注意理解背诵。
inline node *new_(){ node *x=new node; x->ch[0]=x->ch[1]=x->fa=null;x->siz=x->num=1;return x; } inline void insert(int v){ node *x=rt; if(x==null){rt=new_();rt->v=v;return;} node *fa=null; while(x!=null){ fa=x;if(v!=x->v)x=x->ch[v>=x->v]; else {splay(x,null);x->siz++;x->num++;return;} }x=new_();fa->ch[v>=fa->v]=x; x->fa=fa;x->v=v; splay(x,null); }
下一步操作,删除(del,Del)
首先,我们知道,删除的值一定在树中。
于是,我们从根开始搜索。
找到之后,对于这个点,进行del.
先把这个点(x)splay到根,并且把它的子树大小(siz)和同值节点数量(num)--.
这时,有两种结果。
首先,于这个点相同值的点还有。
这样,直接return即可。
否则,如果这棵树只有这一个点,那就把根赋值为null,然后return即可。
否则,顺着x的左右孩子向下找。
找到最后的节点,把它旋转到x的孩子上。
这需要更新x了,也就是删除。
x的孩子认y(转上来的节点)做爹,y是根,爹为null,delete(x)即可。
删除完成。
代码:
inline void del(node *x){ splay(x,null);x->siz--;x->num--;int k; if(x->num)return; if(x->ch[0]!=null)k=0; else if(x->ch[1]!=null)k=1; else {rt=null;delete(x);return;} node *y=x->ch[k]; while(y->ch[k^1]!=null)y=y->ch[k^1]; splay(y,x);y->ch[k^1]=x->ch[k^1]; x->ch[k^1]->fa=y;y->fa=null;rt=y; delete(x); }inline void Del(int v){ node *x=rt; while(x!=null){ if(v!=x->v)x=x->ch[v>=x->v]; else {del(x);return;} } }
然后,就是最熟悉的求排名,求排名为k的数,以及前驱,后继。
rank:首先找v是否存在。不存在输出0.
如果存在,那么它的排名就是当前点的左孩子的子树大小+1.
完成。
求排名为k的数:
定义c为当前点的左子树大小。
如果当前点的左子树大小超过了k,说明它不是要找的点,向它的左子树找。
如果c<k了,说明找到了。
k就把c和当前点的num减掉。
如果k<0了,输出当前x的值即可。
否则,找x的右子树。
完成。
一起说前驱后继吧。
前驱,小于v的最大数。
后继,大于v的最小数。
从根开始搜索,定义一个极值用来更新。
这个不好阐述,看代码理解吧。
上代码:
inline int rank(int v){ node *x=rt; while(x!=null){ if(v>x->v)x=x->ch[1]; else if(v<x->v)x=x->ch[0]; else{splay(x,null);return x->ch[0]->siz+1;} }return 0; }inline int kth(int k){ node *x=rt;int c; while(x!=null){ c=x->ch[0]->siz; if(c>=k)x=x->ch[0]; else{ k-=c+x->num; if(k<=0){splay(x,null);return x->v;} x=x->ch[1]; } }return 0; } inline int pre(int v){ node *x=rt;int ans=-inf; while(x!=null){ if(v>x->v)ans=max(ans,x->v),x=x->ch[1]; else x=x->ch[0]; }return ans; } inline int last(int v){ node *x=rt;int ans=inf; while(x!=null){ if(v<x->v)ans=min(ans,x->v),x=x->ch[0]; else x=x->ch[1]; }return ans; }
至此,Splay告一段落。
Splay被称为序列之王,它还可以实现许多功能。
下次讲树套树的时候,一并说一下。
注:模板来自dalao——wjr.

