72. Edit Distance

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.

You have the following 3 operations permitted on a word:

1. Insert a character
2. Delete a character
3. Replace a character

Example 1:

Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation: 
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')

Example 2:

Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation: 
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')

AC code:

class Solution {
public:
    int minDistance(string word1, string word2) {
        int len1 = word1.length();
        int len2 = word2.length();
        vector<vector<int>> dp(len1+1, vector<int>(len2+1, 0));
        for (int i = 0; i <= len1; ++i) {
            dp[i][0] = i;
        }
        for (int i = 0; i <= len2; ++i) {
            dp[0][i] = i;
        }
        for (int i = 1; i <= len1; ++i) {
            for (int j = 1; j <= len2; ++j) {
                if (word1[i-1] == word2[j-1])
                    dp[i][j] = dp[i-1][j-1];
                else {
                    int flag = min(dp[i-1][j-1], dp[i][j-1]);
                    dp[i][j] = min(flag, dp[i-1][j]) + 1;
                }
            }
        }
        return dp[len1][len2];
    }
};

Runtime: 8 ms, faster than 92.83% of C++ online submissions for Edit Distance.

 

dp[i][j] : the min steps from the position at word1[i] to word2[j] ;

if word[i-1] == word2[j-1]

　　dp[i][j] = dp[i-1][j-1];

else 

　　insert: dp[i][j] = dp[i][j-1] + 1;

　　replace: dp[i][j] = dp[i-1][j-1] + 1;

　　delete: dp[i][j] = dp[i-1][j] + 1;

 

---

2021-04-16

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符
 

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
 

提示：

0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成

题目的实际意义：

　　编辑距离是针对二个字符串（例如英文字）的差异程度的量化量测，量测方式是看至少需要多少次的处理才能将一个字符串变成另一个字符串。编辑距离可以用在自然语言处理中，例如拼写检查可以根据一个拼错的字和其他正确的字的编辑距离，判断哪一个（或哪几个）是比较可能的字。DNA也可以视为用A、C、G和T组成的字符串，因此编辑距离也用在生物信息学中，判断二个DNA的类似程度。Unix 下的 diff 及 patch 即是利用编辑距离来进行文本编辑对比的例子。（来自维基百科）

解题思路：

　　创建一个二维数组dp[i][j]用来表示word1[0-i]与word2[0-j]的编辑距离，那么dp[i][j]就存在两种可能的状态：

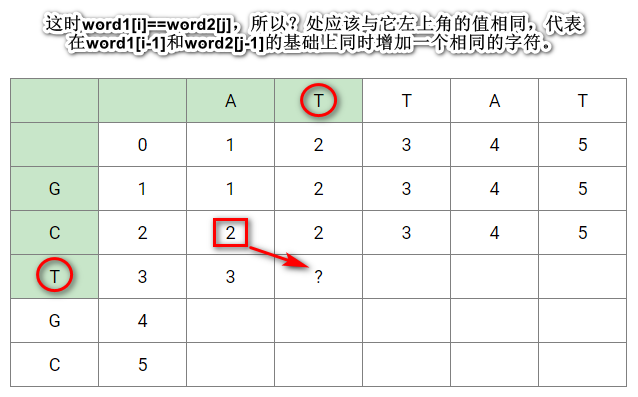
• 如果word1[i] == word2[j]，那么dp[i][j] = dp[i-1][j-1]

 

 

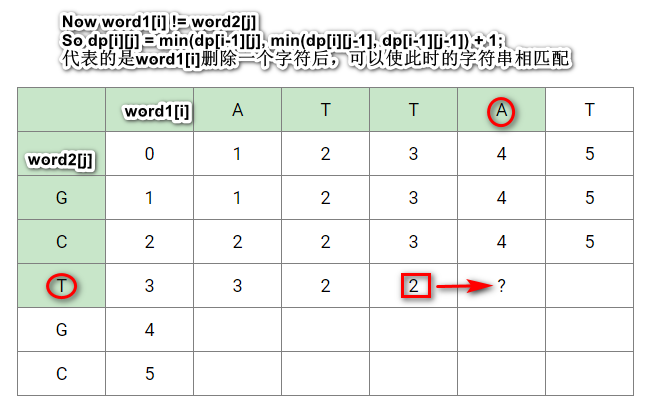
• 如果word1[i] != word2[j]，那么dp[i][j] = min(dp[i-1][j], min(dp[i][j-1], dp[i-1][j-1]) + 1;　　

 

　　还有另外两种情况分别代表的是word2[j]删除一个字符后，可以使两字符串匹配和word1[i] or word2[j]替换一个字符可以使两字符串匹配。

#include <iostream>
#include <vector>

using namespace std;

int main() {
    string s1, s2;
    cin >> s1 >> s2;
    int len1 = s1.length();
    int len2 = s2.length();
    vector<vector<int> > dp(len1 + 1, vector<int>(len2 + 1, 0));
    for (int i = 0; i <= len1; ++i) dp[i][0] = i;
    for (int i = 0; i <= len2; ++i) dp[0][i] = i;
    for (int i = 1; i <= len1; ++i) {
        for (int j = 1; j <= len2; ++j) {
            if (s1[i - 1] == s2[j - 1])
                dp[i][j] = dp[i - 1][j - 1];
            else
                dp[i][j] =
                    min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
        }
    }
    cout << dp[len1][len2] << endl;
    return 0;
}