A - 还是畅通工程(最小生成树)
某省调查乡村交通状况,得到的统计表中列出了任意两村庄间的距离。省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通(但不一定有直接的公路相连,只要能间接通过公路可达即可),并要求铺设的公路总长度为最小。请计算最小的公路总长度。
Input测试输入包含若干测试用例。每个测试用例的第1行给出村庄数目N ( < 100 );随后的N(N-1)/2行对应村庄间的距离,每行给出一对正整数,分别是两个村庄的编号,以及此两村庄间的距离。为简单起见,村庄从1到N编号。
当N为0时,输入结束,该用例不被处理。
Output对每个测试用例,在1行里输出最小的公路总长度。
Sample Input
3 1 2 1 1 3 2 2 3 4 4 1 2 1 1 3 4 1 4 1 2 3 3 2 4 2 3 4 5 0
Sample Output
3
5
Huge input, scanf is recommended.
隔了那么长时间再来做这道题,还是犯了上次同样的错误,初始化parent数组
for(int i = 0; i <= n; i++)
这个地方一定是<=,一直不过真的很不爽,还是自己对代码不熟悉。
AC代码
#include<stdio.h> #include<algorithm> using namespace std; int parent[105]; //定义parent数组用来判断边与边是否形成环路 int sum; struct Edge { int beginn; int endd; int weight; } edges[5005]; bool cmp(Edge a, Edge b) { if(a.weight == b.weight) return a.beginn < b.beginn; else return a.weight < b.weight; } int Find(int f) { while( parent[f] > 0 ) { f = parent[f]; } return f; } //Kruskal算法生成最小生成树 void MiniSpanTree_Kruskal(int x, int y) { int i, n, m; for( i = 0; i <= x; i++ ) { parent[i] = 0; } for( i = 0; i < y; i++ ) { n = Find(edges[i].beginn); m = Find(edges[i].endd); if( n != m ) //如果n==m,则形成环路不满足! { parent[n] = m; //将此边的结尾顶点放入下标为起点的parent数组中,表示此顶点已经在生成树集合中 sum += edges[i].weight; } } printf("%d\n", sum); } int main() { int t, i, ans; while(scanf("%d", &t) != EOF , t) { sum = 0; ans = t*(t - 1)/2; for( i = 0; i < ans; i++ ) { scanf("%d %d %d", &edges[i].beginn, &edges[i].endd, &edges[i].weight); } sort(edges, edges+ans, cmp); MiniSpanTree_Kruskal(t, ans); } return 0; }
还有一种叫做PRIM算法的也可以解这道题。
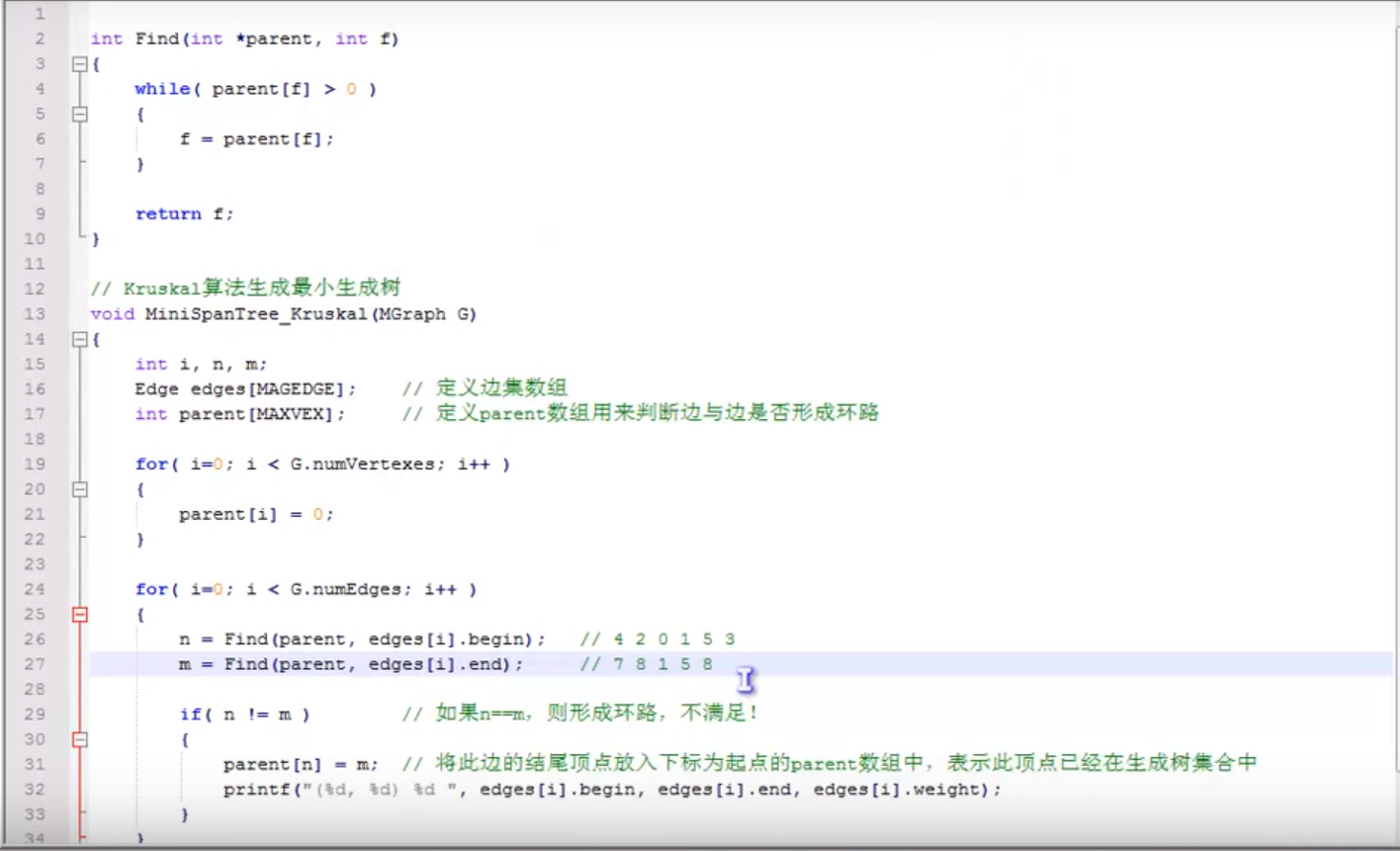
PRIM算法
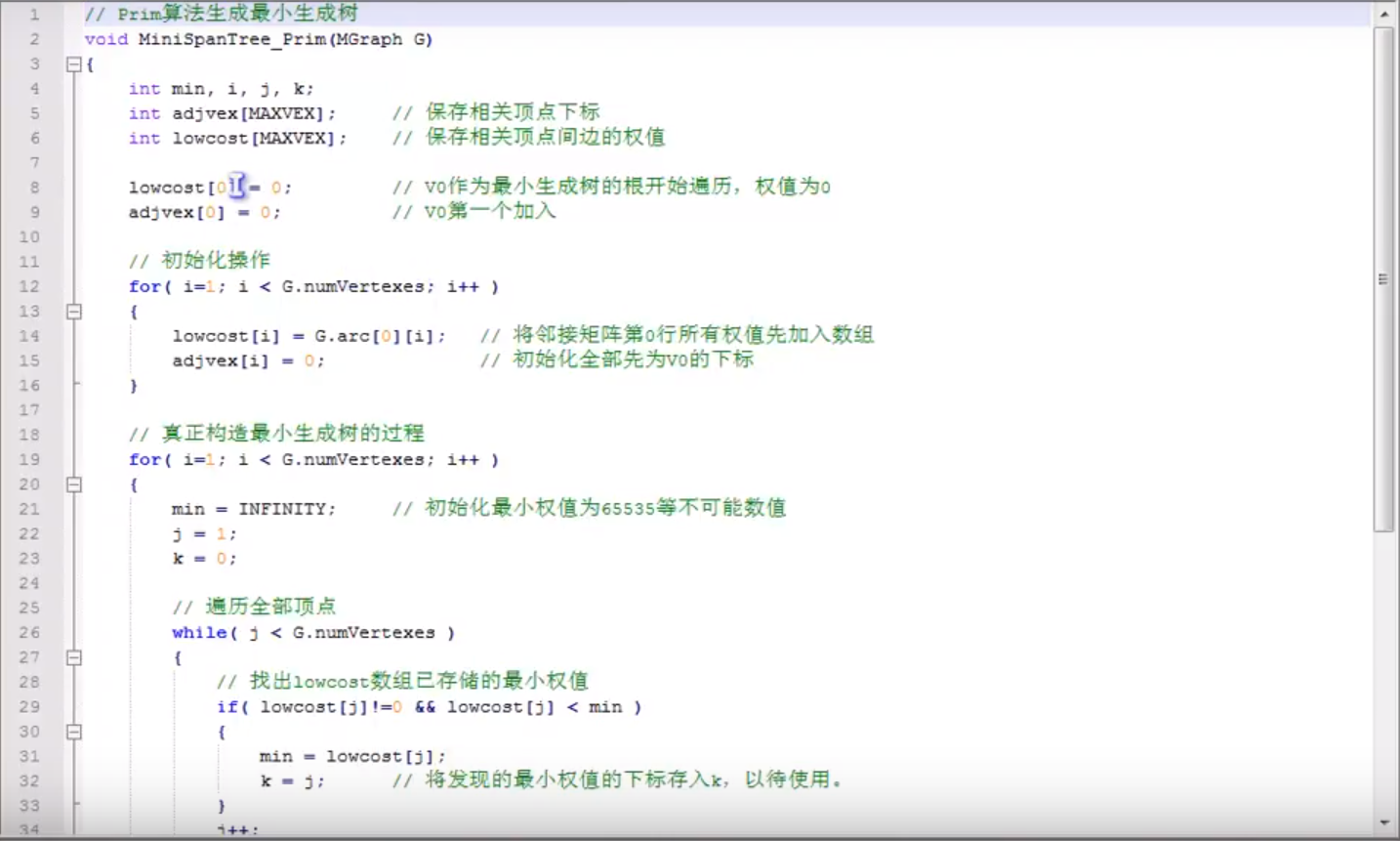
永远渴望,大智若愚(stay hungry, stay foolish)


