蒙特卡洛算法

　　是一种以统计抽样理论为基础，以计算为手段，通过有关随机变量的统计抽样检检验或随机模拟，以求解问题近似解的一种计算方法。

　　求解的步骤：

1. 统计抽样
2. 随机模拟
3. 计算手段
4. 近似解

　　理论方法：大数定律

　　与拉斯维加斯算法的区别：蒙特卡洛算法是尽量找到最优解，不要求一定是最优解（挑苹果问题）；而拉斯维加斯算法必须要给出最优解，如果不是最优解，那么所得到的结果就没有意义（开锁问题）。

　　方法举例：

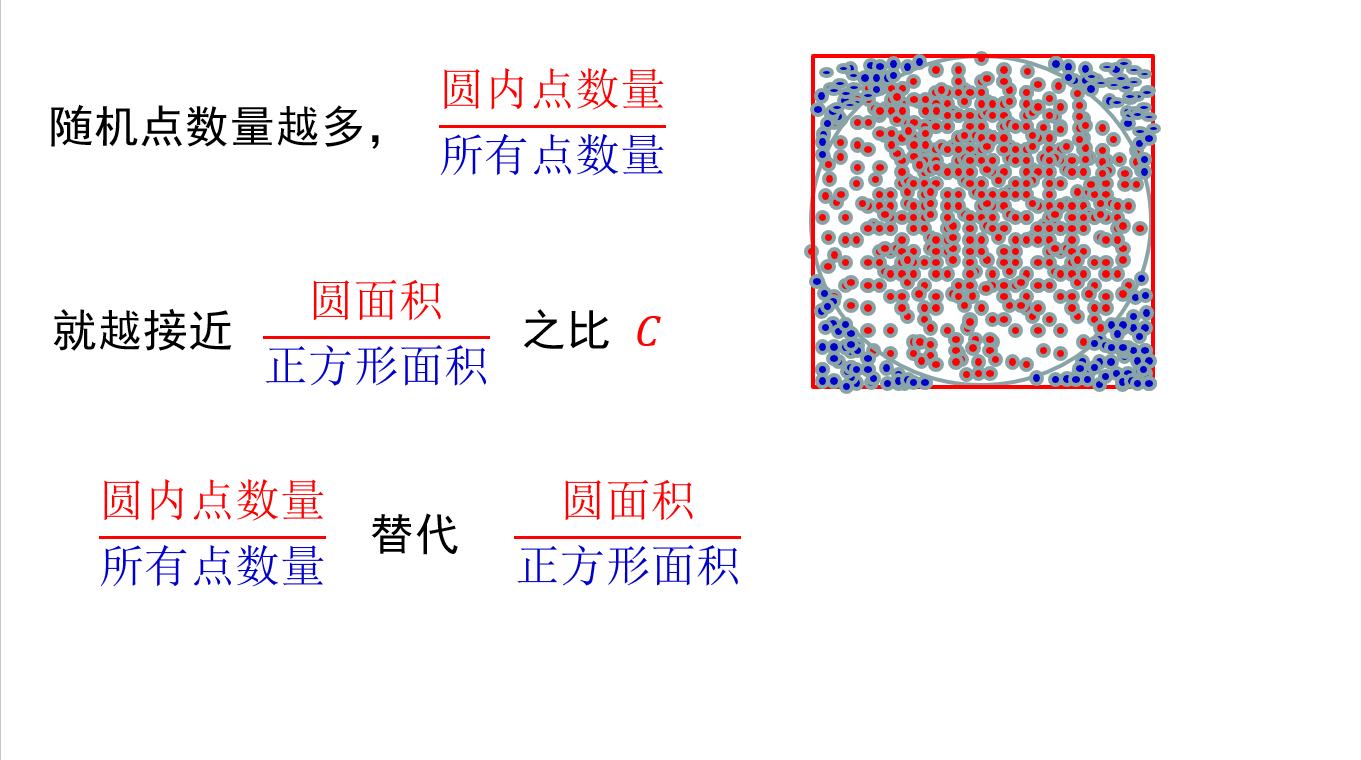
• 圆周率π的计算

 

　　

import random

if __name__ == "__main__":
    count = 0
    for i in range(100000):
        x = random.random()
        y = random.random()
        if (x - 0.5)**2 + (y - 0.5)**2 <= 0.25:
            count += 1
    pi = 4 * (count / 100000)
    print("%.2f" % pi)

　　

 

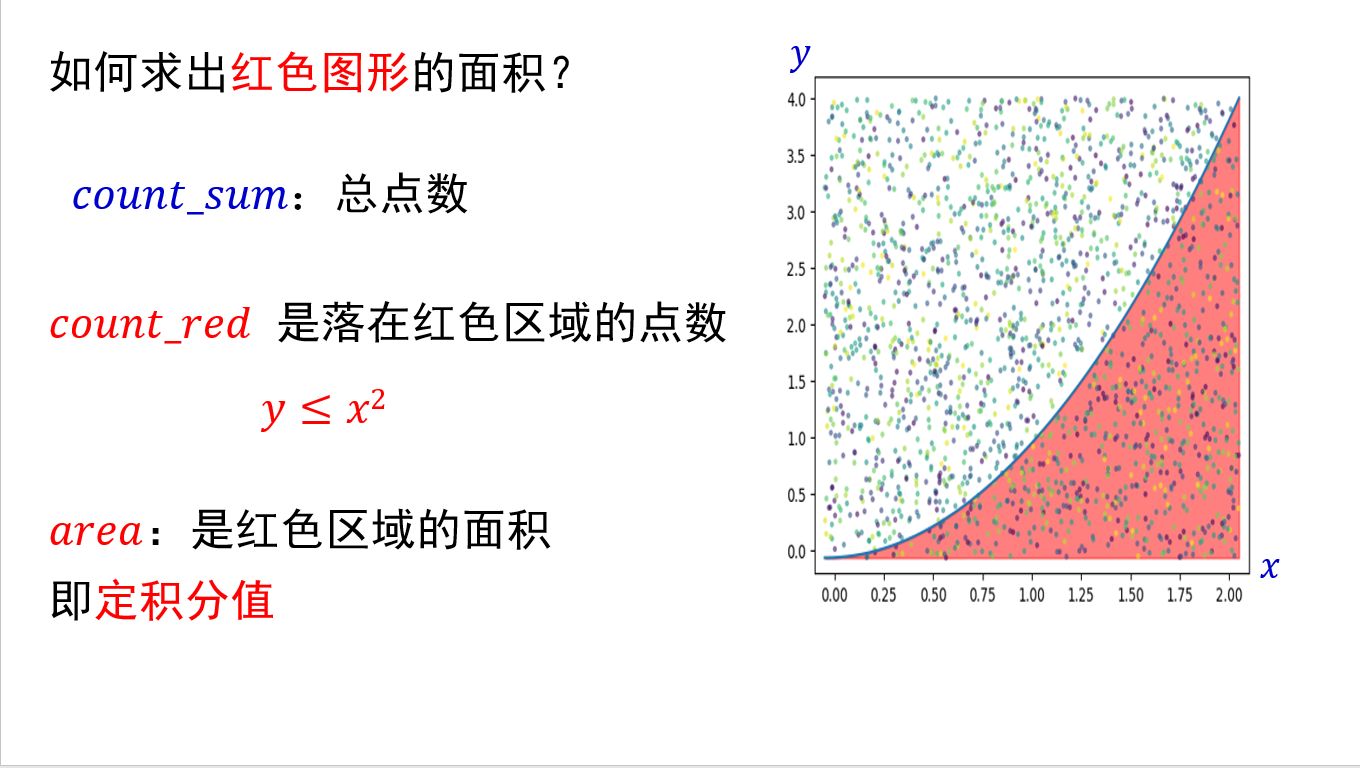
• 蒙特卡洛方法求定积分

 

 

　　

import random

if __name__ == "__main__":
    count = 0
    for i in range(100000):
        x = random.uniform(0, 3)
        y = random.uniform(0, 9)
        if x**2 >= y:
            count += 1
    print("%.1f" % (27 * count / 100000))

　　

 

 

　　方法总结：