1443. Minimum Time to Collect All Apples in a Tree

Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend in order to collect all apples in the tree starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [fromi, toi] means that exists an edge connecting the vertices fromi and toi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple, otherwise, it does not have any apple.

 

Example 1:

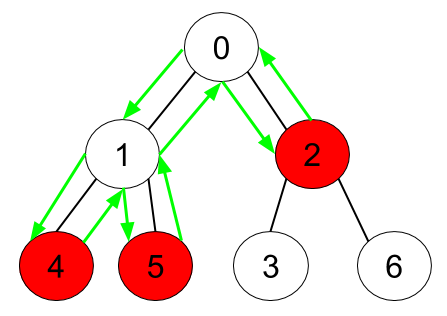
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Example 2:

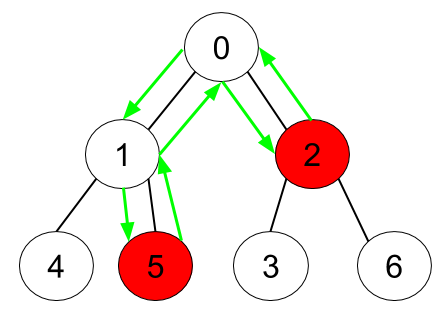
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Example 3:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

 

Constraints:

• 1 <= n <= 10^5
• edges.length == n-1
• edges[i].length == 2
• 0 <= fromi, toi <= n-1
• fromi < toi
• hasApple.length == n

 

题意：

　　给出一棵树，树中某些节点有苹果，求从根节点出发，将所有的苹果收集完，并返回根节点所需的步数。

思路：

　　这是一道DFS的题目，可以把树看成是一个图，然后用DFS遍历图，记录下遍历所需的步数，因为需要返回所以在寻找苹果的过程中，应该将所需的步数 * 2 。这里我们用递归的方法来遍历树，如果子树中没有苹果，则这条遍历路径的步数应该置为0. 否则将遍历到该点所需的步数累加到总步数中。

Code:

class Solution {
public:
    vector<vector<int> > grap;

    int DFS(int index, int mySteps, vector<bool>& hasApple) {
        int childrenSteps = 0;
        for (int i : grap[index]) {
            childrenSteps += DFS(i, 2, hasApple);
        }
        if (childrenSteps == 0 && hasApple[index] == false)
            return 0;
        return childrenSteps + mySteps;
        
    }
    int minTime(int n, vector<vector<int>>& edges, vector<bool>& hasApple) {
        grap.resize(n + 1);
        for (int i = 0; i < edges.size(); ++i) 
            grap[edges[i][0]].push_back(edges[i][1]);
        return DFS(0, 0, hasApple);
    }
};

 

参考：

　　https://leetcode.com/problems/minimum-time-to-collect-all-apples-in-a-tree/discuss/623673/C%2B%2B-Java-Detailed-explanation-with-a-Picture-for-visualization