1053 Path of Equal Weight

Given a non-empty tree with root R, and with weight W​i​​ assigned to each tree node T​i​​. The weight of a path from R to L is defined to be the sum of the weights of all the nodes along the path from R to any leaf node L.

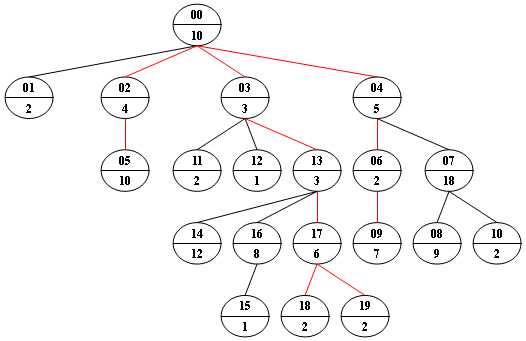
Now given any weighted tree, you are supposed to find all the paths with their weights equal to a given number. For example, let's consider the tree showed in the following figure: for each node, the upper number is the node ID which is a two-digit number, and the lower number is the weight of that node. Suppose that the given number is 24, then there exists 4 different paths which have the same given weight: {10 5 2 7}, {10 4 10}, {10 3 3 6 2} and {10 3 3 6 2}, which correspond to the red edges in the figure.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 0, the number of nodes in a tree, M (<), the number of non-leaf nodes, and 0, the given weight number. The next line contains N positive numbers where W​i​​ (<) corresponds to the tree node T​i​​. Then M lines follow, each in the format:

ID K ID[1] ID[2] ... ID[K]

 

where ID is a two-digit number representing a given non-leaf node, K is the number of its children, followed by a sequence of two-digit ID's of its children. For the sake of simplicity, let us fix the root ID to be 00.

Output Specification:

For each test case, print all the paths with weight S in non-increasing order. Each path occupies a line with printed weights from the root to the leaf in order. All the numbers must be separated by a space with no extra space at the end of the line.

Note: sequence { is said to be greater than sequence { if there exists 1 such that A​i​​=B​i​​ for ,, and A​k+1​​>B​k+1​​.

Sample Input:

20 9 24
10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2
00 4 01 02 03 04
02 1 05
04 2 06 07
03 3 11 12 13
06 1 09
07 2 08 10
16 1 15
13 3 14 16 17
17 2 18 19

 

Sample Output:

10 5 2 7
10 4 10
10 3 3 6 2
10 3 3 6 2

 

题意：

　　给出一棵树，每个节点既有编号又有权值，找出所有从根节点到叶子结点权值之和等于s的所有路径。

思路：

　　构造一个结构体，结构体中既有权重又有孩子结点，同时还有当前结点到达根节点的权重之和。其实寻找路径比较好找，我们用简单的DFS就能够把路径找到，但是问题要求输出的路径按照降序输出，看了别人的代码后，发现，在遍历孩子结点的时候如果我们能够保证孩子结点是由大到小的顺序，那么路径也就一定是由大到小的顺序。明白了只一点，这道题就简单了。

Code：

#include <bits/stdc++.h>

using namespace std;

struct Node {
    int val;
    vector<int> sons;
    int father = -1;
    int sum = 0;
};

vector<int> leaf;
vector<Node> v;

bool cmp(int a, int b) { return v[a].val > v[b].val; }

void DFS(int index, int s) {
    if (v[index].father != -1) {
        int father = v[index].father;
        v[index].sum = v[father].sum + v[index].val;
    }
    if (v[index].sons.size() == 0) {
        if (v[index].sum == s) {
            vector<int> path;
            while (v[index].father != -1) {
                path.push_back(v[index].val);
                index = v[index].father;
            }
            path.push_back(v[index].val);
            reverse(path.begin(), path.end());
            for (int i = 0; i < path.size(); ++i) {
                if (i == 0)
                    cout << path[i];
                else
                    cout << " " << path[i];
            }
            cout << endl;
        }
        return;
    }
    for (int son : v[index].sons) DFS(son, s);
}

int main() {
    int n, m;
    long long s;
    cin >> n >> m >> s;
    v.resize(n);
    for (int i = 0; i < n; ++i) {
        cin >> v[i].val;
        v[i].sum = v[i].val;
    }
    for (int i = 0; i < m; ++i) {
        int index, k, son;
        cin >> index >> k;
        v[index].sum = v[index].val;
        for (int j = 0; j < k; ++j) {
            cin >> son;
            v[index].sons.push_back(son);
            v[son].father = index;
        }
        sort(v[index].sons.begin(), v[index].sons.end(), cmp);
    }
    DFS(0, s);
    return 0;
}