1146 Topological Order

This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.

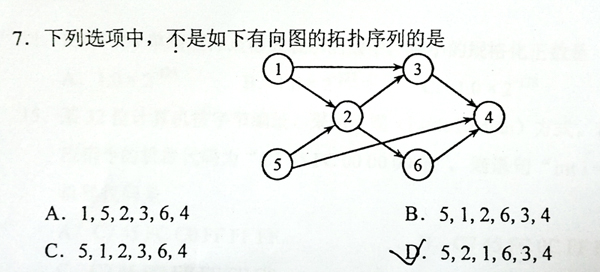
Input Specification:

Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 1,000), the number of vertices in the graph, and M (≤ 10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.

Output Specification:

Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.

Sample Input:

6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6

 

Sample Output:

3 4

 

题意：

　　给出一个拓扑图判断，所给的序列是不是拓扑排序。

思路：

　　用连接矩阵来存储拓扑图，判断是不是拓扑序列的时候，只需要检查还有没有指向这个节点的边。如果没有指向这个节点的边，就将所有以这个结点为起点的边删除。

 

Code：

#include <iostream>
#include <queue>
#include <vector>

using namespace std;

int main() {
    int n, m;
    cin >> n >> m;

    int s, e;
    vector<vector<int> > grap(n + 1, vector<int>(n + 1, 0));
    for (int i = 0; i < m; ++i) {
        cin >> s >> e;
        grap[s][e] = 1;
    }

    int k, t;
    cin >> k;
    bool isTopo = true;
    vector<int> ans;
    vector<vector<int> > dummy;
    for (int i = 0; i < k; ++i) {
        isTopo = true;
        dummy = grap;
        for (int j = 0; j < n; ++j) {
            cin >> t;
            for (int k = 1; k <= n; ++k) {
                if (dummy[k][t] != 0)
                    isTopo = false;
                else {
                    dummy[t][k] = 0;
                }
            }
        }
        if (!isTopo) ans.push_back(i);
    }
    cout << ans[0];
    for (int i = 1; i < ans.size(); ++i) {
        cout << " " << ans[i];
    }
    cout << endl;

    return 0;
}

 

上面的代码最后一组数据超时，又优化了一下代码，通过了全部的测试点。

#include <iostream>
#include <queue>
#include <vector>

using namespace std;

int main() {
    int n, m;
    cin >> n >> m;

    int s, e;
    vector<vector<int> > grap(n + 1, vector<int>(n + 1, 0));
    for (int i = 0; i < m; ++i) {
        cin >> s >> e;
        grap[s][e] = 1;
    }

    int k, t;
    cin >> k;
    vector<int> ans, temp;
    vector<vector<int> > dummy;
    for (int i = 0; i < k; ++i) {
        dummy = grap;
        temp.clear();
        for (int j = 0; j < n; ++j) {
            cin >> t;
            temp.push_back(t);
        }
        bool flag = false;
        for (int j = 0; j < n; ++j) {
            for (int k = 1; k <= n; ++k) {
                if (dummy[k][temp[j]] == 1) {
                    flag = true;
                    ans.push_back(i);
                    break;
                } else
                    dummy[temp[j]][k] = 0;
            }
            if (flag) break;
        }
    }
    cout << ans[0];
    for (int i = 1; i < ans.size(); ++i) {
        cout << " " << ans[i];
    }
    cout << endl;

    return 0;
}

 

---

参考了一下别人的代码，变更了一种解体的思路，代码也更加的简洁。

#include <iostream>
#include <queue>
#include <vector>

using namespace std;

int main() {
    int n, m;
    cin >> n >> m;

    int s, e;
    vector<int> v[n+1], in(n+1, 0);
    for (int i = 0; i < m; ++i) {
        cin >> s >> e;
        v[s].push_back(e);
        in[e]++;
    }
    int k, t;
    cin >> k;
    vector<int> ans;
    for (int i = 0; i < k; ++i) {
        bool flag = true;
        vector<int> temp = in;
        for (int j = 0; j < n; ++j) {
            cin >> t;
            if (temp[t] != 0) flag = false;
            for (int it : v[t]) 
                temp[it]--;
        }
        if (!flag) ans.push_back(i);
    }

    int isFirst = true;
    for (int i = 0; i < ans.size(); ++i) {
        if (isFirst) {
            cout << ans[i];
            isFirst = false;
        } else {
            cout << " " << ans[i];
        }
    }

    return 0;
}

　　这种方法是通过记录每个节点的入度，根据遍历的过程中是否有入度不为0的结点来判断所给序列是不是拓扑排序。