Weekly Contest 132

1025. Divisor Game

Alice and Bob take turns playing a game, with Alice starting first.

Initially, there is a number N on the chalkboard.  On each player's turn, that player makes a move consisting of:

• Choosing any x with 0 < x < N and N % x == 0.
• Replacing the number N on the chalkboard with N - x.

Also, if a player cannot make a move, they lose the game.

Return True if and only if Alice wins the game, assuming both players play optimally.

 

Example 1:

Input: 2
Output: true
Explanation: Alice chooses 1, and Bob has no more moves.

Example 2:

Input: 3
Output: false
Explanation: Alice chooses 1, Bob chooses 1, and Alice has no more moves.

 

Note:

1. 1 <= N <= 1000

 

Approach #1: Math. [Java]

class Solution {
    public boolean divisorGame(int N) {
        if (N % 2 == 0) return true;
        else return false;
    }
}

　　

1026. Maximum Difference Between Node and Ancestor

Given the root of a binary tree, find the maximum value V for which there exists different nodes A and B where V = |A.val - B.val| and A is an ancestor of B.

(A node A is an ancestor of B if either: any child of A is equal to B, or any child of A is an ancestor of B.)

 

Example 1:

Input: [8,3,10,1,6,null,14,null,null,4,7,13]
Output: 7
Explanation: 
We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.

 

Note:

1. The number of nodes in the tree is between 2 and 5000.
2. Each node will have value between 0 and 100000.

 

Approach #1: [Java]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int maxAncestorDiff(TreeNode root) {
        return dfs(root, root.val, root.val);
    }
    
    public int dfs(TreeNode root, int mx, int mn) {
        if (root == null) return 0;
        int res = Math.max(root.val - mn, mx - root.val);
        mx = Math.max(mx, root.val);
        mn = Math.min(mn, root.val);
        res = Math.max(res, dfs(root.left, mx, mn));
        res = Math.max(res, dfs(root.right, mx, mn));
        return res;
    }

}

　　

1027. Longest Arithmetic Sequence

Given an array A of integers, return the length of the longest arithmetic subsequence in A.

Recall that a subsequence of A is a list A[i_1], A[i_2], ..., A[i_k] with 0 <= i_1 < i_2 < ... < i_k <= A.length - 1, and that a sequence B is arithmetic if B[i+1] - B[i] are all the same value (for 0 <= i < B.length - 1).

 

Example 1:

Input: [3,6,9,12]
Output: 4
Explanation: 
The whole array is an arithmetic sequence with steps of length = 3.

Example 2:

Input: [9,4,7,2,10]
Output: 3
Explanation: 
The longest arithmetic subsequence is [4,7,10].

Example 3:

Input: [20,1,15,3,10,5,8]
Output: 4
Explanation: 
The longest arithmetic subsequence is [20,15,10,5].

 

Note:

1. 2 <= A.length <= 2000
2. 0 <= A[i] <= 10000

 

Approach #1: [Java]

class Solution {
    public int longestArithSeqLength(int[] A) {
        if (A.length <= 1) return A.length;
        int longest = 0;
        Map<Integer, Integer>[] dp = new HashMap[A.length];
        for (int i = 0; i < A.length; ++i)
            dp[i] = new HashMap<Integer, Integer>();
        for (int i = 1; i < A.length; ++i) {
            for (int j = 0; j < i; ++j) {
                int d = A[i] - A[j];
                int len = 2;
                if (dp[j].containsKey(d)) {
                    len = dp[j].get(d) + 1;
                }
                int curr = dp[i].getOrDefault(d, 0);
                dp[i].put(d, Math.max(len, curr));
                longest = Math.max(longest, dp[i].get(d));
            }
        }
        return longest;
    }
}

 

Analysis:

We iteratively build the map for a new index i, by considering all elements to the left one-by-one. For each pair of indeces (i, j) and difference d = A[i] - A[j] considered, we check if there was an existing chain at the index j with difference d always.

If yes, we can then extend the existing chain length by 1.

Else, if not, then we can start a new chain of length 2 with this new difference d and (A[j], A[i]) as its elements.

At the end, we can then return the maximum chain length that we have seen so far.　

 

1028. Recover a Tree From Preorder Traversal

We run a preorder depth first search on the root of a binary tree.

At each node in this traversal, we output D dashes (where D is the depth of this node), then we output the value of this node.  (If the depth of a node is D, the depth of its immediate child is D+1.  The depth of the root node is 0.)

If a node has only one child, that child is guaranteed to be the left child.

Given the output S of this traversal, recover the tree and return its root.

 

Example 1:

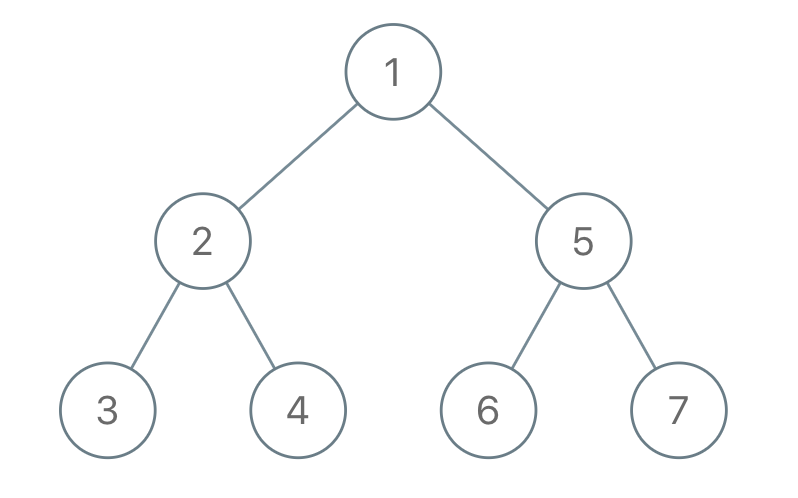
Input: "1-2--3--4-5--6--7"
Output: [1,2,5,3,4,6,7]

Example 2:

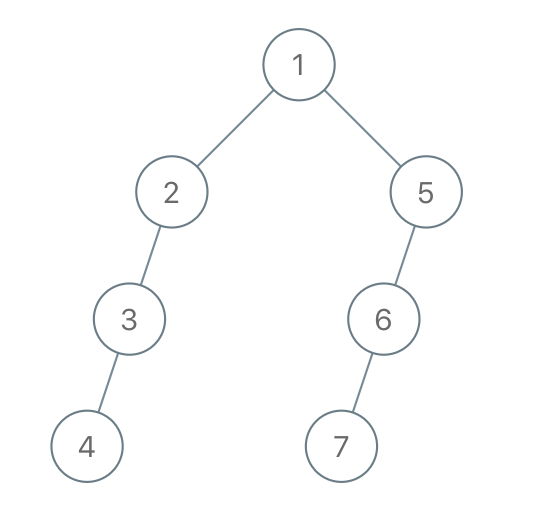
Input: "1-2--3---4-5--6---7"
Output: [1,2,5,3,null,6,null,4,null,7]

 

Example 3:

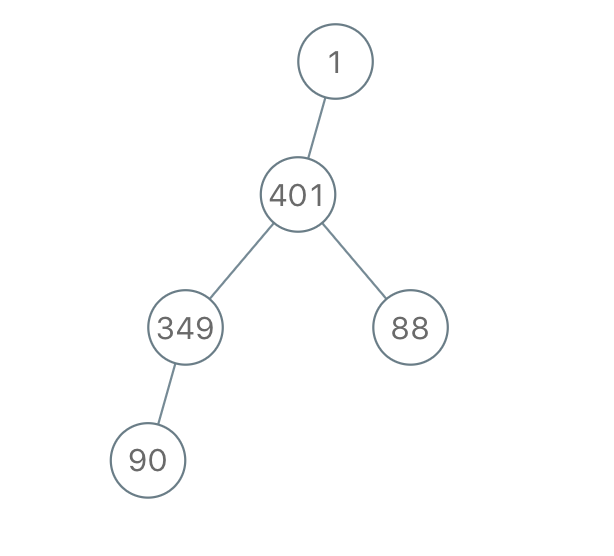
Input: "1-401--349---90--88"
Output: [1,401,null,349,88,90]

 

Note:

• The number of nodes in the original tree is between 1 and 1000. 
• Each node will have a value between 1 and 10^9.

 

Approach #1: [Java]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    int index = 0;
    public TreeNode recoverFromPreorder(String S) {
        return helper(S, 0);
    }
    
    public TreeNode helper(String s, int depth) {
        int numDash = 0;
        while (index + numDash < s.length() && s.charAt(index+numDash) == '-') {
            numDash++;
        }
        if (numDash != depth) return null;
        int next = index + numDash;
        while (next < s.length() && s.charAt(next) != '-') next++;
        int val = Integer.parseInt(s.substring(index + numDash, next));
        index = next;
        TreeNode root = new TreeNode(val);
        root.left = helper(s, depth + 1);
        root.right = helper(s, depth + 1);
        return root;
    }
}