139. Word Break

Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, determine if s can be segmented into a space-separated sequence of one or more dictionary words.

Note:

• The same word in the dictionary may be reused multiple times in the segmentation.
• You may assume the dictionary does not contain duplicate words.

Example 1:

Input: s = "leetcode", wordDict = ["leet", "code"]
Output: true
Explanation: Return true because "leetcode" can be segmented as "leet code".

Example 2:

Input: s = "applepenapple", wordDict = ["apple", "pen"]
Output: true
Explanation: Return true because "applepenapple" can be segmented as "apple pen apple".
             Note that you are allowed to reuse a dictionary word.

Example 3:

Input: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
Output: false

 

Approach #1: 

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> _wordDict(wordDict.begin(), wordDict.end());
        return wordBreak(s, _wordDict);
    }
    
    bool wordBreak(const string& s, const unordered_set<string>& wordDict) {
        if (memo_.count(s)) return memo_[s];
        if (wordDict.count(s)) return memo_[s] = true;
        for (int j = 1; j < s.length(); ++j) {
            string left = s.substr(0, j);
            string right = s.substr(j);
            if (wordDict.count(right) && wordBreak(left, wordDict))
                return memo_[s] = true;
        }
        return memo_[s] = false;
    }
    
private:
    unordered_map<string, bool> memo_;
};

　　

---

2021-04-17

给定一个非空字符串 s 和一个包含非空单词的列表 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
示例 1：

输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
示例 2：

输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
  注意你可以重复使用字典中的单词。
示例 3：

输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false

 

思路：

　　运用dp的思想，先判断子问题是否满足条件，然后再将当前问题拆分成若干子问题，如果拆分成的子问题都满足条件，那么当前问题也是满足条件的。

 

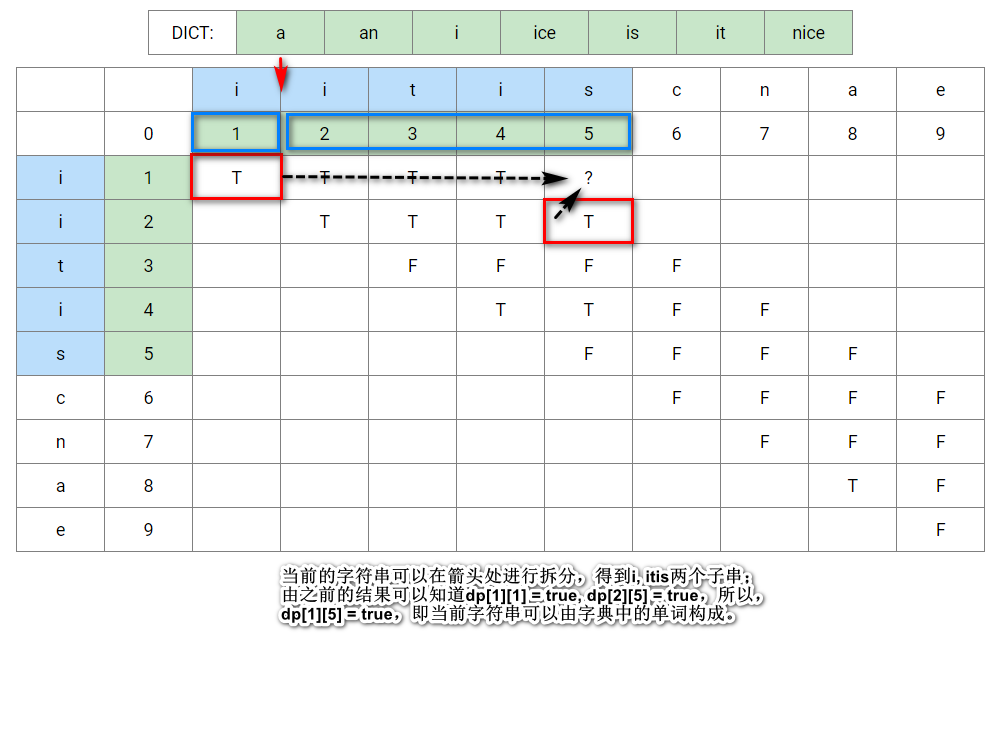
代码：

#include <iostream>
#include <set>
#include <string>
#include <vector>

using namespace std;

int main() {
    string input;
    set<string> s;
    cin >> input;
    int n;
    string t;
    cin >> n;
    for (int i = 0; i < n; ++i) {
        cin >> t;
        s.insert(t);
    }
    int len = input.length();
    vector<vector<bool> > dp(len + 1, vector<bool>(len + 1, false));
    for (int l = 1; l <= len; ++l) {
        for (int i = 0, j = i + l - 1; j < len; ++i, ++j) {
            string sub = input.substr(i, l);
            if (s.find(sub) != s.end())
                dp[i][j] = true;
            else {
                for (int k = 1; k < l; ++k) {
                    int t = i + k;
                    if (dp[i][i + k - 1] && dp[t][j]) {
                        dp[i][j] = true;
                        break;
                    }
                }
            }
        }
    }
    cout << dp[0][len - 1] << endl;
    return 0;
}

 

---

2021-08-03

今天刷题的时候又遇到了这道题目，因为如果之前写过的话会留下之前的代码，所以就看着之前的代码重新复习了一下。

动态规划的定义：把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

动态规划的思想：把原问题拆分为具有相同结构和性质的子问题，根据子问题的解来求解当前的问题。动态规划是一种自底向上（down-top）的解法，与之相对应的是递归解法（top-down）。

动态规划的应用场景：

• 最优子结构性质：
• 无后效性：
• 子问题重叠性质：

按照我自己的理解，动态规划一般都要维护一个二维的dp数组，判断子问题是否满足条件。当求一个大的问题的时候，当子问题满足条件，当新增加一个元素后，判断新加入的元素是否满足条件。这样就可以不必理会子问题，只需要判断新加入的元素是否满足条件。