【数据结构】堆

一、堆介绍

　　堆是具有以下性质的完全二叉树：

• 每个结点的值都大于或等于其左右孩子结点的值， 称为最大堆(大顶堆)，

• 每个结点的值都小于或等于其左右孩子结点的值， 称为最小堆(小顶堆),

• 注意 : 没有要求结点的左孩子的值和右孩子的值的大小关系。

　　完全二叉树：一棵深度为 k 的有 n 个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为 i（1≤i≤n）的结点与满二叉树中编号为 i 的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树

　　以下是最小堆的示例图

　　

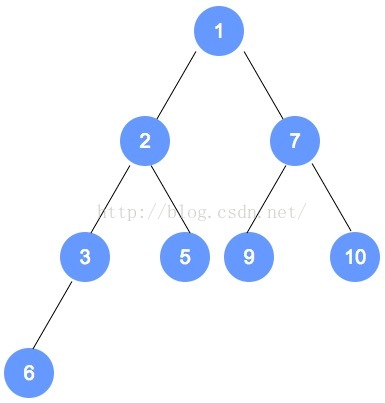
二、堆操作

　　以最小堆为例

2.1 最小堆的构建

　　初始数组为：[9, 3, 7, 6, 5, 1, 10, 2]

构建步骤

　　1、按照完全二叉树，将数字依次填入，填入后，找到最后一个结点（本示例为数字2的节点），从它的父节点（本示例为数字6的节点）开始调整。

　　2、调整时，父节点小于两个子节点中较小的那个，则将父节点与较小的子节点互换，即以父节点下浮操作

      3、以递归被互换的子节点，以互换的子节点为父节点进行调整，直到没有子节点时结束，也就是这一轮调整结束

      4、第二轮调整，是数字6的节点数组下标小1的节点（比数字6的下标小1的节点是数字7的节点），用刚才的规则进行调整。以此类推，直到调整到根节点。

图释

• 找到最后一个结点的节点
  

　　

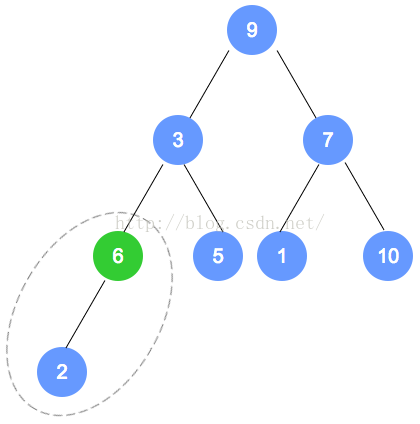
• 第一次调整了 2 和 6，由于调整后 6 无子节点，则第一轮调整结束

• 进行第二轮调整，找到原数字6的节点数组下标小1的节点（7节点）

　　

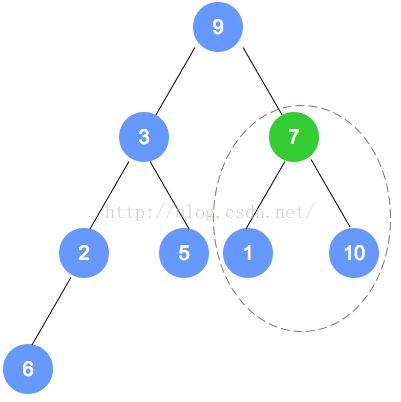
• 第二轮调整了 1 和 7 ，然后结束第二轮调整，进行下一下轮，从 3 节点开始

　　

　　

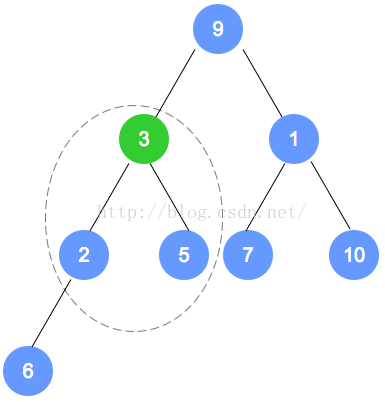
• 第三轮调整了 2 和 3 ，调整后，3 有子节点，继续向下调整，由于 3 小于 6，无需改变，结束第三轮调整

• 然后进行下一下轮，从 9 节点开始

　　

　　

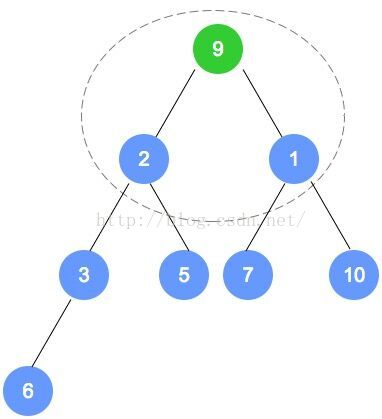
• 第四轮调整了 1 和 9 ，调整后，9 有子节点，继续向下调整

　　　　

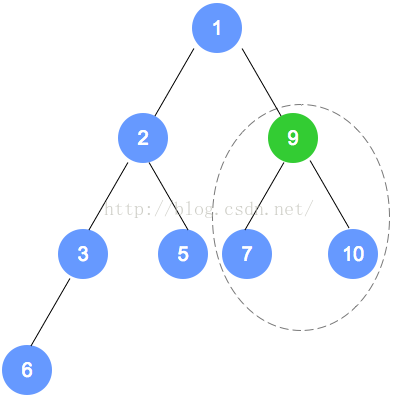
• 第四轮的第二次调整了 7 和 9 ，调整后，9 无子节点，第四轮调整结束

　　

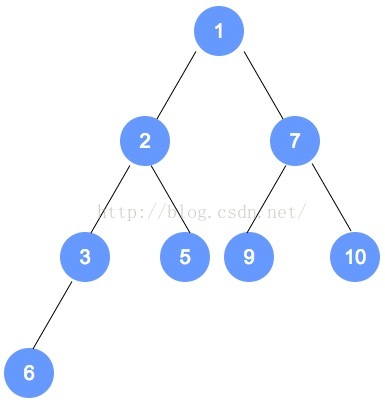
2.2 最小堆的元素插入

　　以上个最小堆为例，插入数字0。

插入步骤

       1、数字0的节点首先加入到该二叉树最后的一个节点，

　　2、依据最小堆的定义，自底向上，递归调整。

插入操作的图解

• 数字0的节点首先加入到该二叉树最后的一个节点

　　

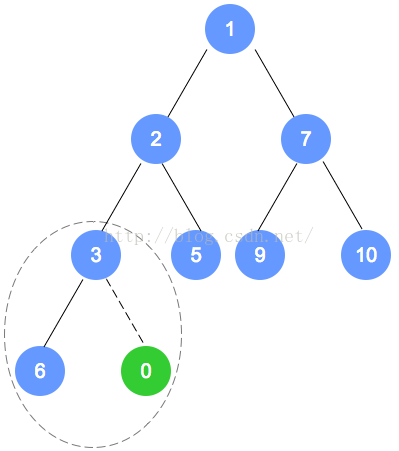
• 调整 0 与 3 的位置，然后递归向上调整以0为子节点

　　

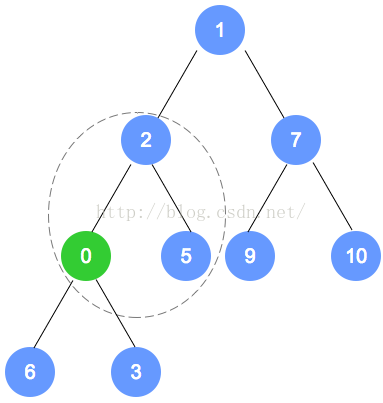
• 调整 0 与 2 的位置，然后递归向上调整以0为子节点

　　

　　

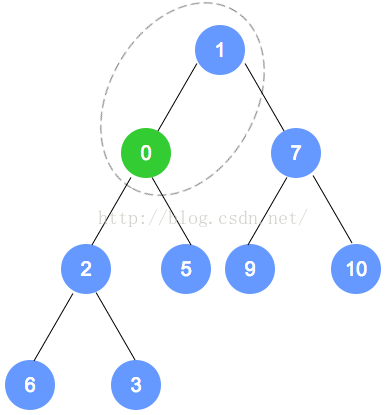
• 调整 0 与 1 的位置，调整结束

　　

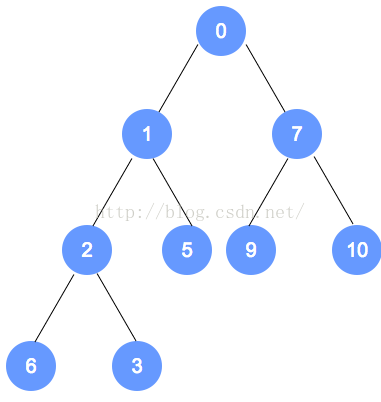
2.3 最小堆的节点删除

　　对于最小堆和最大堆而言，删除是针对于根节点而言。

删除步骤：

　　1、对于删除操作，将二叉树的最后一个节点替换到根节点，

　　2、然后自顶向下，递归调整。

以下是图解：

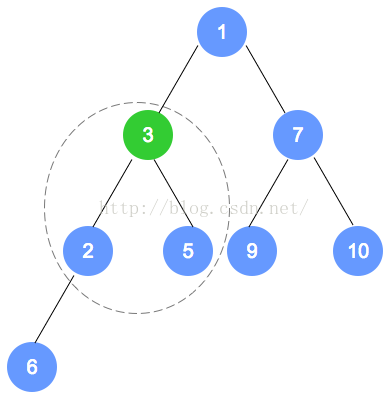
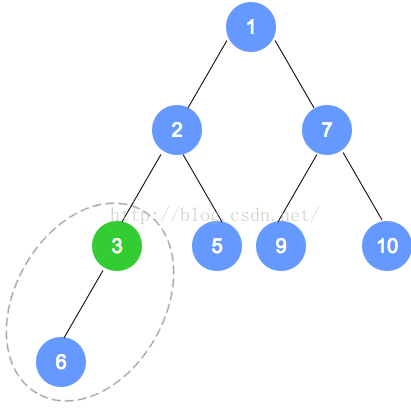
• 将二叉树的最后一个节点替换到根节点

　　

　　

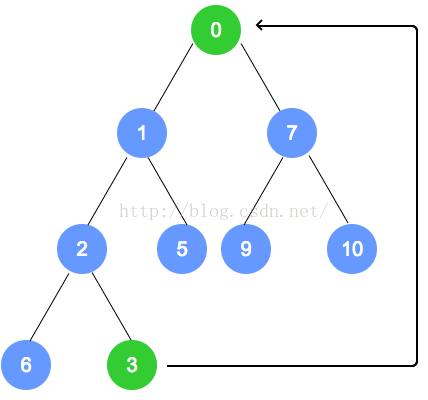
• 自顶向下，递归调整。

　　 

　　

　　

三、代码实现

3.1 最小堆代码

/**
 * 最小堆
 */
public class MinHeap {

    /**
     * 最小堆构建
     */
    public void initMinHeap(int[] arr) {
        if (arr == null || arr.length <= 1) {
            return;
        }
        System.out.println("原 arr = " + Arrays.toString(arr));
        // 遍历单次上浮
        siftUpLoop(arr);
    }

    /**
     * 遍历单次上浮
     * 根据父节点进行上浮
     */
    public void siftUpLoop(int[] arr) {

        // 从最后一个代子节点的树开始
        int parent = (arr.length - 1 - 1) / 2;
        // 遍历
        for (; parent >= 0; parent--) {
            siftDown(arr, parent);
            System.out.println("arr = " + Arrays.toString(arr));
        }
    }

    /**
     * 最小堆的元素插入
     */
    public int[] insertToMinHeap(int[] arr, int val) {
        // 复制生成 lenth + 1 长度的数组
        int[] nums = Arrays.copyOf(arr, arr.length + 1);
        // 将插入元素放到数组最后
        nums[nums.length - 1] = val;

        System.out.println("新数组 nums = " + Arrays.toString(nums));

        // 循环上浮最后一个元素
        siftUp(nums, nums.length - 1);
        return nums;
    }

    /**
     * 循环上浮
     * 根据当前节点进行上浮
     */
    public void siftUp(int[] arr, int index) {
        while (index > 0) {
            int parent = (index - 1) / 2;
            // 将父节点 与 当前节点  进行比较
            if (arr[parent] > arr[index]) {
                // 进行交换
                swap(arr, parent, index);
                // 循环父级
                index = parent;
            } else {
                break;
            }
        }
    }
    public int[] deletFromMinHeap(int[] arr) {
        // 将数组中最后一个元素赋值给  arr[0]
        arr[0] = arr[arr.length - 1];
        // 删除最后一个数，得到新数组
        int[] nums = Arrays.copyOf(arr,  arr.length - 1);
        System.out.println("新数组 nums = " + Arrays.toString(nums));

        // 循环下浮元素
        siftDown(nums, 0);
        return nums;
    }

    private void siftDown(int[] arr, int current) {

        while (current < arr.length / 2) {
            int left = 2 * current + 1;
            int right = 2 * current + 2;

            int min = left;
            // 存在右节点情况
            if(right < arr.length && arr[left] > arr[right]) {
                min = right;
            }
            // 将当前节点 与 两个子节点中较小的节点  进行比较
            if (arr[current] > arr[min]) {
                // 当前节点值大于较小值，则进行交换
                swap(arr, current, min);
                // 循环子节点
                current = min;
            }else {
                break;
            }
        }

    }

    public void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    public static void main(String[] args) {
        int[] arr = {9, 3, 7, 6, 5, 1, 10, 2};
        MinHeap minHeap = new MinHeap();
        // 初始化最小堆
        minHeap.initMinHeap(arr);
        System.out.println("arr = " + Arrays.toString(arr));
        // 最小堆的元素插入
        int[] addToMinHeap = minHeap.insertToMinHeap(arr, 0);
        System.out.println("最小堆的元素插入 = " + Arrays.toString(addToMinHeap));
        // 最小堆的节点删除
        int[] deletMinHeap = minHeap.deletFromMinHeap(addToMinHeap);
        System.out.println("最小堆的节点删除 = " + Arrays.toString(deletMinHeap));
    }

}　　

3.2 最大堆代码 

/**
 * 最大堆
 */
public class MaxHeap {

    /**
     * 最大堆构建
     */
    public void initMaxHeap(int[] arr) {
        if (arr == null || arr.length <= 1) {
            return;
        }
//        System.out.println("原 arr = " + Arrays.toString(arr));
        // 遍历单次上浮
        siftUpLoop(arr);
    }

    /**
     * 遍历单次上浮
     * 根据父节点进行上浮
     */
    public void siftUpLoop(int[] arr) {

        // 从最后一个代子节点的树开始
        int parent = (arr.length - 1 - 1) / 2;
        // 遍历
        for (; parent >= 0; parent--) {
            siftDown(arr, parent);
//            System.out.println("arr = " + Arrays.toString(arr));
        }
    }

    /**
     * 最大堆的元素插入
     */
    public int[] insertToMaxHeap(int[] arr, int val) {
        // 复制生成 lenth + 1 长度的数组
        int[] nums = Arrays.copyOf(arr, arr.length + 1);
        // 将插入元素放到数组最后
        nums[nums.length - 1] = val;

        System.out.println("新数组 nums = " + Arrays.toString(nums));

        // 循环上浮最后一个元素
        siftUp(nums, nums.length - 1);
        return nums;
    }

    /**
     * 循环上浮
     * 根据当前节点进行上浮
     */
    public void siftUp(int[] arr, int index) {
        while (index > 0) {
            int parent = (index - 1) / 2;
            // 将父节点 与 当前节点  进行比较
            if (arr[parent] < arr[index]) {
                // 进行交换
                swap(arr, parent, index);
                // 循环父级
                index = parent;
            } else {
                break;
            }
        }
    }
    public int[] deletFromMaxHeap(int[] arr) {
        // 将数组中最后一个元素赋值给  arr[0]
        arr[0] = arr[arr.length - 1];
        // 删除最后一个数，得到新数组
        int[] nums = Arrays.copyOf(arr,  arr.length - 1);
        System.out.println("新数组 nums = " + Arrays.toString(nums));

        // 循环下浮元素
        siftDown(nums, 0);
        return nums;
    }

    private void siftDown(int[] arr, int current) {

        while (current < arr.length / 2) {
            int left = 2 * current + 1;
            int right = 2 * current + 2;

            int max = left;
            // 存在右节点情况
            if(right < arr.length && arr[left] < arr[right]) {
                max = right;
            }
            // 将当前节点 与 两个子节点中较大的节点  进行比较
            if (arr[current] < arr[max]) {
                // 当前节点值大于较大值，则进行交换
                swap(arr, current, max);
                // 循环子节点
                current = max;
            }else {
                break;
            }
        }

    }

    public void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    public static void main(String[] args) {
        int[] arr = {9, 3, 7, 6, 5, 1, 10, 2};
        MaxHeap maxHeap = new MaxHeap();
        // 初始化最大堆
        maxHeap.initMaxHeap(arr);
        System.out.println("arr = " + Arrays.toString(arr));
        // 最大堆的元素插入
        int[] addToMaxHeap = maxHeap.insertToMaxHeap(arr, 0);
        System.out.println("最大堆的元素插入 = " + Arrays.toString(addToMaxHeap));
        // 最大堆的节点删除
        int[] deletMaxHeap = maxHeap.deletFromMaxHeap(addToMaxHeap);
        System.out.println("最大堆的节点删除 = " + Arrays.toString(deletMaxHeap));
    }

}

 

　　参考：https://blog.csdn.net/hrn1216/article/details/51465270